HEXADECIMAL TO DECIMAL BINARY OCTAL CONVERTER

The online tool provided in this section can be used to convert hexadecimal to decimal, binary and octal. 

What is decimal, binary, octal and hexadecimal?

Decimal :

Decimal is nothing but the number we use in our day to day life. Whatever number we write in our day to day life, we use the ten digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Since we use one or some of these ten digits in decimal, we say  that  decimal is having base 10.

Binary :

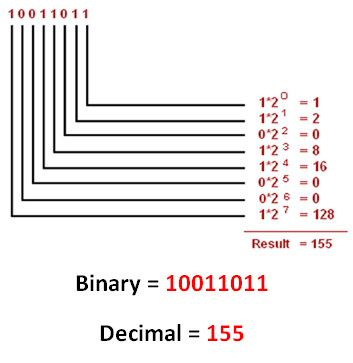
In digital electronics, we write the numbers using only the two digits "0" and "1". Whatever number we we have in regular, it will be written in digital electronics only by using the two digits "0" and "1".

Since we use only the two digits "0" and "1" in binary, we say that binary is having base 2.

Octal :

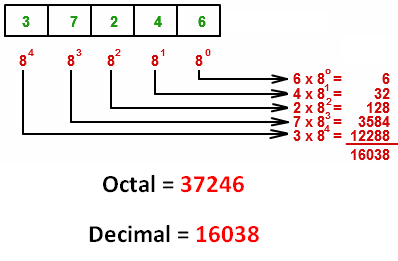
Octal is nothing but the number we write using the eight digits 0, 1, 2, 3, 4, 5, 6, 7.

Since  we use one or some of these eight digits in octal, we say  that octal is having base 8.  

Hexadecimal :

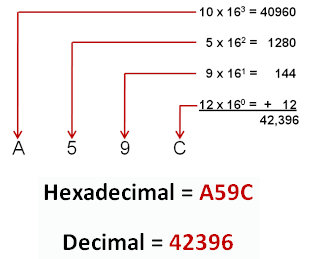
Hexadecimal is nothing but the number we write using the sixteen digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

Here,

A  =  10, B  =  11, C  =  12, D  =  13, E  =  14, F  =  16

Whatever number we have in regular, it will be written in hexadecimal using these 16 digits.

Since we use one or some of these 16 digits in hexadecimal, we say that hexadecimal is having base 16.

The above explanation of decimal, binary, octal and hexadecimal is clearly shown in the picture below. 

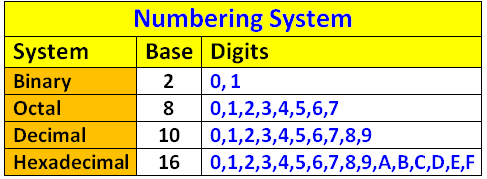
Conversions Between Decimal, Binary, Octal and Hexadecimal

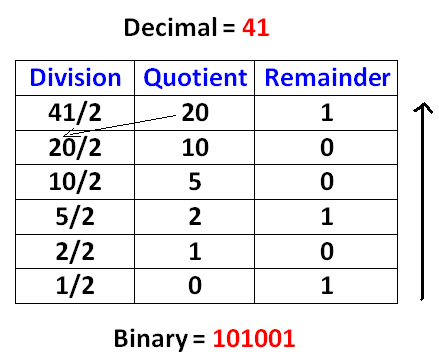
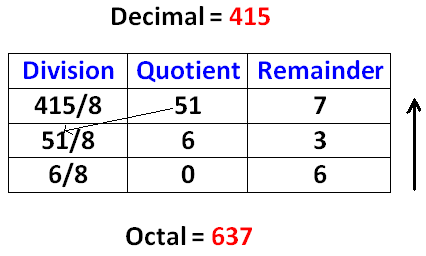
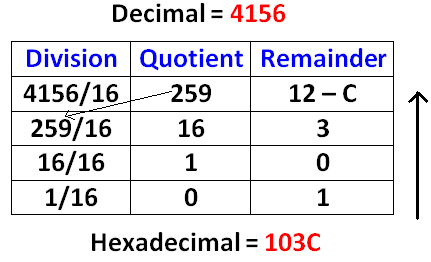
Decimal to Binary Conversion Decimal to Octal Conversion Decimal to Hexadecimal Conversion Binary to Decimal Conversion Octal to Decimal Conversion Hexadecimal to Decimal Conversion

View Example View Example View Example View Example View Example View Example

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.