HEIGHT AND DISTANCE PROBLEMS IN TRIGONOMETRY

To know how to solve height and distance problems in trigonometry, we must be knowing the following basic stuff in trigonometry. 

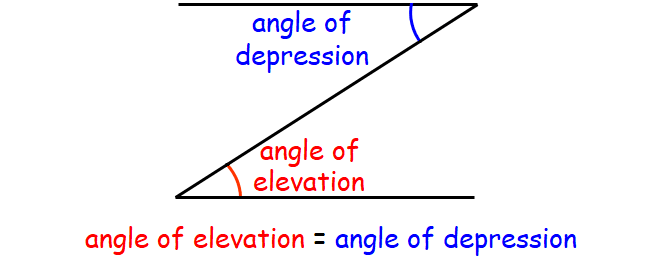
Angle of Elevation and Angle of Depression

Trigonometric Ratios

opp ----> opposite side

hyp ----> hypotenuse

adj ----> adjacent side

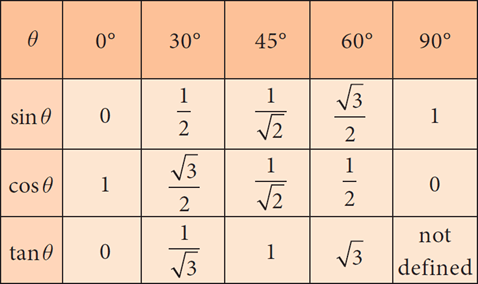
Trigonometric ratios of angles 0°, 30°, 45°, 60° and 90°.

Practice Problems

Problem 1 : 

The angle of elevation of the top of the building at a distance of 50 m from its foot on a horizontal plane is found to be 60°. Find the height of the building.

Solution :

Draw a sketch.

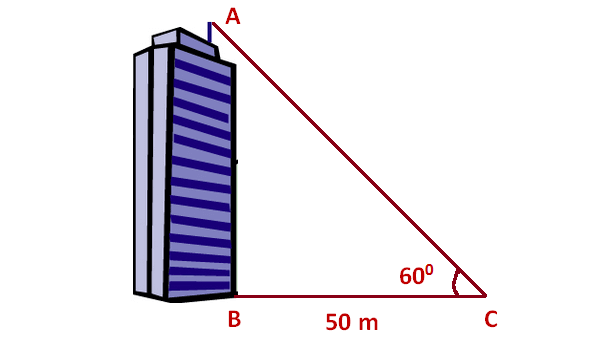
Here, AB represents height of the building, BC represents distance of the building from the point of observation.

In the right triangle ABC, the side which is opposite to the angle 60° is known as opposite side (AB), the side which is opposite to 90° is called hypotenuse side (AC) and the remaining side is called adjacent side (BC).

Now we need to find the length of the side AB.

Multiply both sides by 50.

50√3 = AB

Approximate value of √3 is 1.732.

AB  50(1.732)

     AB ≈ 86.6

So, the height of the building is about 86.6 m.

Problem 2 :

A ladder placed against a wall such that it reaches the top of the wall of height 6 m and the ladder is inclined at an angle of 60°. Find how far the ladder is from the foot of the wall.

Solution :

Draw a sketch.

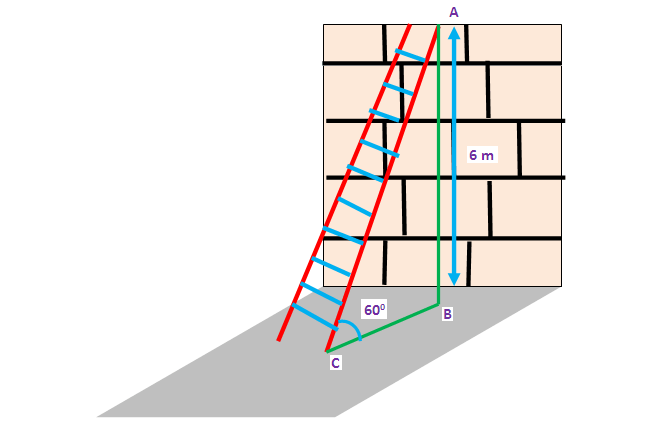
Here AB represents height of the wall, BC represents the distance between the wall and the foot of the ladder and AC represents the length of the ladder.

In the right triangle ABC, the side which is opposite to angle 60° is known as opposite side (AB), the side which is opposite to 90° is called hypotenuse side (AC) and remaining side is called adjacent side (BC).

Now, we need to find the distance between foot of the ladder and the wall. That is, we have to find the length of BC.

BC = 2√3

BC ≈ 2(1.732)

BC ≈ 3.464

So, the distance between foot of the ladder and the wall is about 3.464 m.

Problem 3 :

A string of a kite is 100 meters long and it makes an angle of 60° with horizontal. Find the height of the kite, assuming that there is no slack in the string.

Solution :

Draw a sketch.

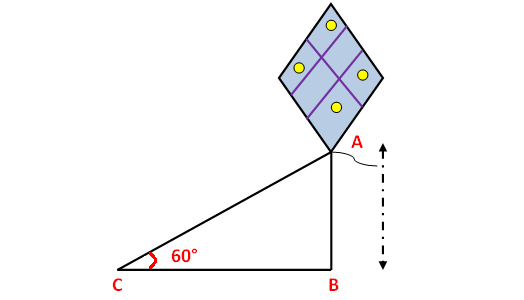
Here AB represents height of kite from the ground, BC represents the distance of kite from the point of observation.

In the right triangle ABC the side which is opposite to angle 60° is known as opposite side (AB), the side which is opposite to 90° is called hypotenuse side (AC) and remaining side is called adjacent side (BC).

Now we need to find the height of the side AB.

AB ≈ 50√3

AB ≈ 50(1.732)

AB ≈ 86.6

So, the height of kite from the ground is about 86.6 m.

Problem 4 :

From the top of the tower 30 m height a man is observing the base of a tree at an angle of depression measuring 30°. Find the distance between the tree and the tower.

Solution :

Draw a sketch. 

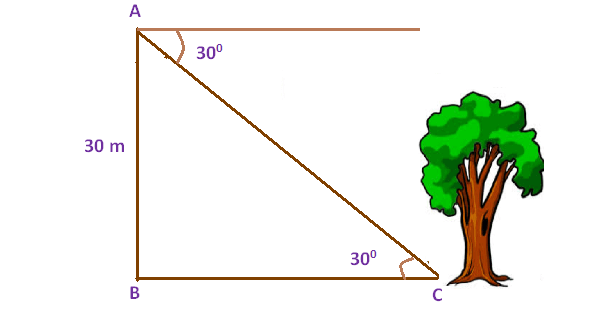
Here AB represents height of the tower, BC represents the distance between foot of the tower and the foot of the tree. 

Now we need to find the distance between foot of the tower and the foot of the tree (BC).

BC = 30√3

BC = 30(1.732)

 BC = 51.96

So, the distance between the tree and the tower is about 51.96 m.

Problem 5 :

A man wants to determine the height of a light house. He measured the angle at A and found that tan A = 3/4. What is the height of the light house if A is 40 m from the base?

Solution :

Draw a sketch.

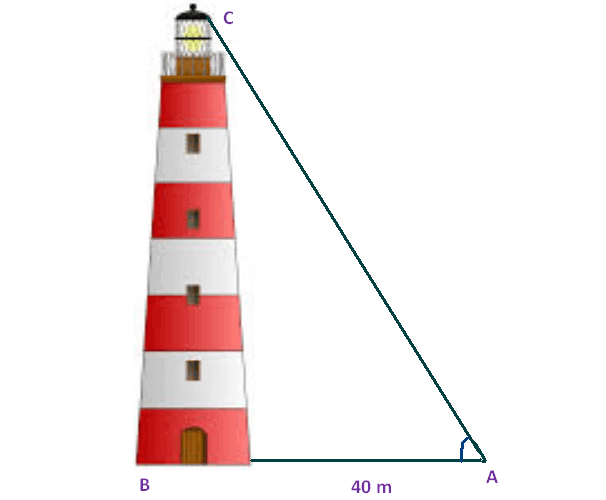
Here BC represents height of the light house, AB represents the distance between the light house from the point of observation. 

In the right triangle ABC the side which is opposite to the angle A is known as opposite side (BC), the side which is opposite to 90° is called hypotenuse side (AC) and remaining side is called adjacent side (AB).

Now we need to find the height of the light house (BC).

30 = BC 

So, the height of the light house is 30 m.

Problem 6 :

The length of a string between a kite and a point on the ground is 90 m. If the string is making an angle θ with the level ground  such that tan θ = 15/8, how high will the kite be ?

Solution :

Draw a sketch.

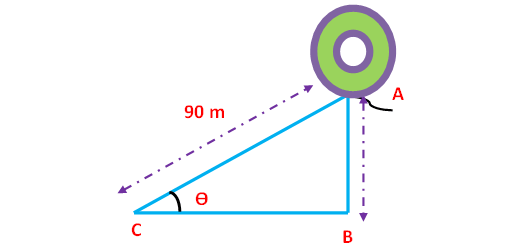
Here AB represents height of the balloon from the ground. In the right triangle ABC the side which is opposite to angle θ is known as opposite side (AB), the side which is opposite to 90° is called hypotenuse side (AC) and remaining side is called adjacent side (BC).

Now we need to find the length of the side AB.

tanθ = ¹⁵⁄₈ -----> cotθ = ⁸⁄₁₅

Then, we have

AB ≈ 79.41

So, the height of the tower is about 79.41 m.

Problem 7 :

An aero plane is observed to be approaching the air point. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 50°. Find the height above the ground.

Solution :

Draw a sketch. 

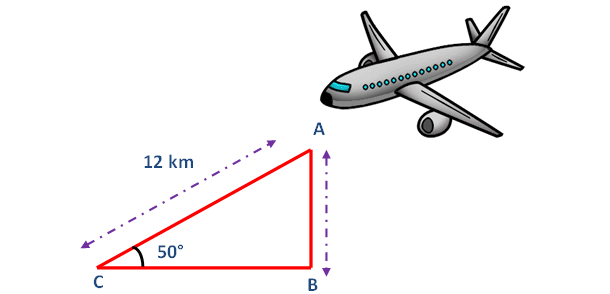
Here AB represents height of the airplane from the ground. In the right triangle ABC the side which is opposite to angle 50° is known as opposite side (AB), the side which is opposite to 90° is called hypotenuse side (AC) and remaining side is called adjacent side (BC).

Now we need to find the length of the side AB.

From the figure given above, AB stands for the height of the aero plane above the ground. 

AB ≈ 9.192 km

So, the height of the aero plane above the ground is about 9.192 km.

Problem 8 :

A balloon is connected to a meteorological station by a cable of length 200 m inclined at 60° angle . Find the  height of the balloon from the ground. (Imagine that there is no slack in the cable)

Solution :

Draw a sketch.

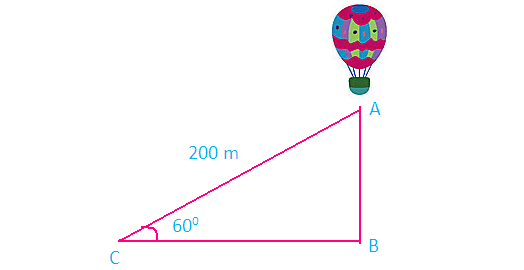
Here AB represents height of the balloon from the ground. In the right triangle ABC the side which is opposite to angle 60° is known as opposite side (AB), the side which is opposite to 90° is called hypotenuse (AC) and the remaining side is called as adjacent side (BC).

Now we need to find the length of the side AB.

From the figure given above, AB stands for the height of the balloon above the ground. 

AB = 100√3

AB ≈ 100(1.732)

AB ≈ 173.2

So, the height of the balloon from the ground is about 173.2 m.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.