HCF AND LCM WORD PROBLEMS WORKSHEET

Problem 1 :

Two numbers are in the ratio 2 : 3. If the second number is 51, find their HCF.

Problem 2 :

Two number are in the ratio 3 : 5 and their HCF is 5. Find the numbers.

Problem 3 :

Two number are in the ratio 3 : 25 and their LCM is 150. Find the numbers.

Problem 4 :

Two numbers are in the ratio 4 : 5 and their sum is 36. Find their least common multiple.

Problem 5 :

Every 7 years the Lancaster family has a family reunion. Every 6 years they update their family tree. If they both had a photo taken and updated their family tree in 2008, in what year will both events occur again ?

Problem 6 :

Abraham has two pieces of wire, one 6 feet long and the other 12 feet long. If he wants to cut them up to produce many pieces of wire that are all of the same length, with no wire left over, what is the greatest length, in feet, that he can make them ?

Answers

1. Answer :

Because the two numbers are in the ratio 2 : 3, the numbers can be assumed as 2x and 3x.

Find the HCF of 2x and 3x.

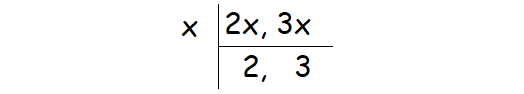
The common factor of 2x and 3x is x.

HCF (2x, 3x) = x

But, it is given that the second number is 51.

3x = 51

x = 17

So, the HCF of the two numbers is 17.

2. Answer :

Because the two numbers are in the ratio 3 : 5, the numbers can be assumed as 3x and 5x.

HCF (3x, 5x) = x

But, it is given that the greatest common factor of the two numbers is 5.

x = 5

Substitute x = 5 in 3x and 5x.

3x = 3(5) = 15

5x = 5(5) = 25

So, the two numbers are 15 and 25.

3. Answer :

Because the two numbers are in the ratio 3 : 25, the numbers can be assumed as 3x and 25x.

LCM (3x, 25x) = 75x

But, it is given that the least common multiple of the two numbers is 150.

75x = 150

x = 2

Substitute x = 2 in 3x and 25x.

3x = 3(2) = 6

25x = 25(2) = 50

So, the two numbers are 6 and 50.

4. Answer :

Because the two numbers are in the ratio 4 : 5, the numbers can be assumed as 4x and 5x.

4x + 5x = 36

9x = 36

x = 4

Substitute x = 4 in 5x and 6x.

4x = 4(4) = 16

5x = 5(4) = 20

The two numbers are 16 and 20.

LCM (16, 20) = 80

5. Answer :

For example, let the family has reunion after every 3 years and update their family tree after every 4 years.

Then the Lancaster family would have reunion after 3, 6, 9, 12 years......

Like this, the family would update their family tree after 4, 8, 12, 16 years......

If they both have a photo taken and updated their family tree now, again both the events will occur after 12 years. This 12 is the least common multiple (LCM) of 3 and 4.

The same thing happened in our problem. To find the year both events occur again, we have to find the LCM of 7 and 6.

LCM (7, 6) = 42 years

If both events occur in 2008, again they occur after 42 years.

= 2008 + 42

= 2050

In 2050 both events will occur again.

5. Answer :

When the two wires are cut in to small pieces, each piece must of same length and also it has to be the possible greatest length.

6 feet wire can be cut in to pieces of (2, 2, 2) or (3, 3).

12 feet wire can be cut in to pieces of

(2, 2, 2, 2, 2, 2 ) or (3, 3, 3, 3)

The length of each small piece must be of possible greatest length.

To find the possible greatest length, we have to find the greatest number which can divide both 6 and 12. That is the highest common factor of (6, 12).

HCF (6, 12) = 6

Hence, the greatest length of each small piece will be 6 ft.

(That is, 6 feet wire is not cut in to small pieces and it is kept as it is. Only the 12 feet wire is cut in to 2 pieces at the length of 6 feet/piece)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.