HCF AND LCM PROBLEMS

Problem 1 :

Find the highest common factor (HCF) of the numbers 48 and 64 using division method.

Solution :

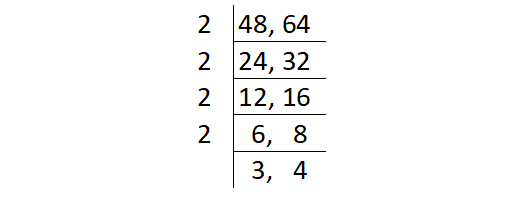
The product of common factors of 48 and 64 is

= 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2

= 16

So, HCF (48, 64) = 16.

Problem 2 :

Find the highest common factor of the numbers 18, 24 and 30 by factor tree method.

Solution :

Using  factor Tree Method, find the factors of 18, 24 and 30.

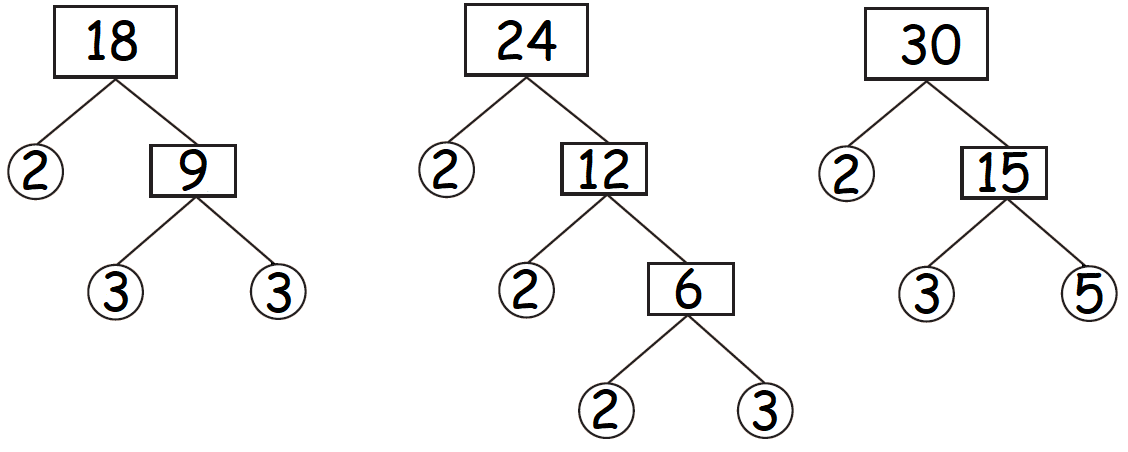
The factors of 18 are 1, 2, 3, 6, 9 and 18.

The factors of 24 are  1, 2, 3, 4, 6, 8, 12 and 24.

The factors of 30 are  1, 2, 3, 5, 6, 10, 15 and 30.

The factors that are common to all numbers 18, 24 and 30 are

1, 2, 3, 6

In the above common factors, 6 is the largest value.

So, HCF (18, 24, 30) = 6.

Problem 3 :

Find the highest common factor of the numbers 84 and 182 by prime factorization method.

Solution :

Write the prime factors of 84 and 182 as shown below.

84 = 2 ⋅ 7 ⋅ 2 ⋅ 3

182 = 2 ⋅ 7 ⋅ 13

The prime factors that are common to 84 and 182 are

2 and 7

Product of common prime factors :

= 2 ⋅ 7

So, HCF (84, 182) = 14.

Problem 4 :

What is the greatest number that will divide 62, 78 and 109 leaving remainders 2, 3 and 4 respectively ?

Solution :

When 62, 78 and 109 are divided by the greatest number, leaving remainders 2, 3 and 4 respectively.

62 - 2 = 60

78 - 3 = 75

109 - 4 = 105

Get all the common factors of 60, 75 and 105 and see that the common factors will divide them all. The greatest number is the HCF of 60, 75 and 105.

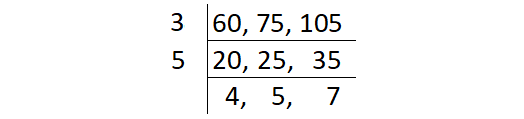
The product of common factors of 60, 75 and 105 is

= 3 ⋅ 5

= 15

So, HCF (60, 75, 105) = 15.

Hence, the HCF is 15, which is the greatest number that will divide 62, 78, 109 leaving remainders 2, 3 and 4 respectively.

Problem 5 :

Find the highest common factor of the numbers 0.045 and 0.075.

Solution :

In the given two numbers 0.045 and 0.075, we find equal number of digits after the decimal point. That is, three digits.

To get rid of the decimal point, we have to multiply each number by 1000.

0.045 ⋅ 1000 = 45

0.075 ⋅ 1000 = 75

Find the greatest common factor 45 and 75 using prime factorization method.

Write the prime factors of 45 and 75 as shown below.

45 = 3 ⋅ 3 ⋅ 5

75 = 3 ⋅ 5 ⋅ 5

The prime factors that are common to 45 and 75 are

3 and 5

Product of common prime factors :

= 3 ⋅ 5

= 15

HCF (45, 75) = 15.

Divide the HCF 15 by 1000.

15/1000 = 0.015

So, the greatest common factor of 0.045 and 0.075 is

0.015

Problem 6 :

Find the least common multiple (LCM) of 7 and 12.

Solution :

There is no common divisor for 7 and 12.

So, 7 and 12 are relatively prime.

The least common multiple of two numbers that are relatively prime is product of those two numbers.

Hence, the least common multiple of 7 and 12 is

= 7 ⋅ 12

= 84

Problem 7 :

Find the least common multiple of 18 and 24 using prime factorization method.

Solution :

Write the prime factors of 18 and 24.

18 = 2 ⋅ 3 ⋅ 3

24 = 2 ⋅ 2 ⋅ 2 ⋅ 3

The prime factor 2 appears a maximum of 3 times in the prime factorization of 24.

The prime factor 3 appears a maximum of 2 times in the prime factorization of 18.

LCM (18, 24) = 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3

= 72

Problem 8 :

Find the least common multiple of 6, 7 and 15 by division method.

Solution :

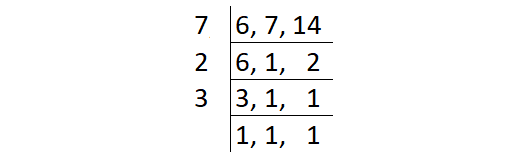
LCM (6, 7, 14) = Product of all prime factors

= 7 ⋅ 2 ⋅ 3

= 42

Problem 9 :

Two numbers are in the ratio 7 : 9 and their least common multiple is 378. Find the numbers.

Solution :

Because the two numbers are in the ratio 7 : 9, the numbers can be assumed as 7x and 9x.

Find the least common multiple of 7x and 9x.

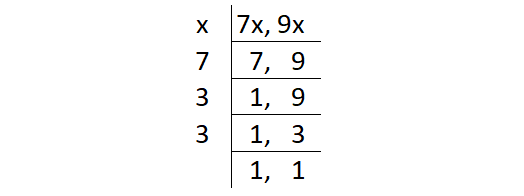
LCM (7x, 9x) = x ⋅ 7 ⋅ 3 ⋅ 3

= 63x

But, it is given that the least common multiple of the two numbers is 378.

63x = 378

Divide each side by 63.

x = 6

Substitute x = 8 in 7x and 9x.

7x = 7(6) = 42

9x = 9(6) = 54

So, the two numbers are 42 and 54.

Problem 10 :

Find the least common multiple of the following two fractions.

8/21, 6/35

Solution :

Formula to find the least common multiple of fractions :

= LCM of Numerators / HCF of Denominators

*LCM -----> least common multiple

*HCF -----> highest common factor

LCM of numerators (8, 6) = 24

HCF of denominators (21, 35) = 7

Least common multiple of (8/21, 6/35) is

= 24/7

Problem 11 :

The LCM of two numbers is 432 and their HCF is 36. If one of the numbers is 108, then find the other number.

Solution :

Let x be the other number.

We know that, the product of the two numbers is

= LCM ⋅ HCF

108 ⋅ x = 432 ⋅ 36

Divide each side by 108.

x = (432 ⋅ 36)/108

x = 144

The other number is 144.

Problem 12 :

The LCM of two co-prime numbers is 5005. If one of the numbers is 65, then find the other number.

Solution :

Let x be the other number.

We know that, the product of the two numbers is

= LCM ⋅ HCF

As the HCF of co-primes is 1,

65 ⋅ x = 5005 ⋅ 1

65x = 5005

Divide each side by 65.

x = 77

The other number is 77.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.