HALF ANGLE IDENTITIES IN TRIGONOMETRY

Example 1 :

Using half angle find the value of sin 15°

Solution :

We may write, 15°  =  30°/2

So,

sin 15°  =  sin (30°/2)

We know that,

sin²A/2  =  (1-cosA)/2

sin (A/2)  =  √ (1-cosA)/2

sin (30°/2)  =  √[(1-cos 30)/2]

=  √[(1-√3/2)/2]

=  √[(2-√3)/4]

=  √(2-√3)/2

Example 2 :

Using half angle formula find the value of tan 15°

Solution :

15°  =  30°/2

So, tan 15°  =  tan 30°/2

tan²(A/2)  =  (1-cos A)/(1+cos A)

tan(A/2)  =  √(1-cos A)/(1+cos A)

tan 30°/2  =  √[(1-cos 30°)/(1+cos 30°)]

=  √[(1-√3/2)/(1+√3/2)]

=  √[( 2-√3 )/2] x [2/(2+√3)] 

=  √(2-√3)/(2+√3) 

Rationalizing the denominator,

=  √[(2-√3)²/(2² - (√3)²]

=  √[(2²+(√3)² - 2(2)(√3) /(2² - (√3)²]

=  √[(2²+(√3)² - 2(2)(√3) /(4-3]

=  √[(2-√3)² /1]

=  √[(2-√3)²

=  2-√3

So, the value of tan 15° is 2-√3.

Example 3 :

Using half angle find the value of cos 15°

Solution :

15°  =  30°/2

So, cos 15°  =  cos 30°/2

cos²A/2  =  (1+cos A)/2

cos (A/2)  =  √(1+cos A)/2

cos 30°/2   =  √[(1+cos 30)/2]

=  √[(1+√3/2)/2]

=  √[(2+√3)/4]

=  √(2+√3)/2

Example 4 :

Find the exact value of cos 105°

Solution :

105°  =  210°/2

From cos 2A = 2cos² A - 1,

cos² A = (1 + cos 2A) / 2

cos A = √[(1 + cos 2A) / 2]

Dividing the angle by 2, we get 

cos (A/2) = √[(1 + cos A) / 2]

cos (210/2) = √[(1 + cos 210) / 2] ----(1)

Angle 210 lies in 3rd quadrant,

cos 210 = cos (180 + 30)

= -cos 30

= -√3/2

By applying the value of cos 210 in (1), we get

= √[(1 + (-√3/2)) / 2]

= √[(2 - √3)/4]

= √(2 - √3)/2

Example 5 :

If sin a = -3/5 and 180 < a < 270, find the exact value of 

i) cos (a/2)     ii)  tan (a/2)

Solution :

sin a = -3/5

From sin² a + cos² a = 1

cos² a = 1 - sin² a

cos a = √(1 - sin² a)

= √(1 - (-3/5)²)

= √(1 - (9/25))

= √(25 - 9)/25

= √(16/25)

Since the angle a lies in 3^rd quadrant,

cos a = -4/5

cos (a/2) = -√[(1 + cos a) / 2]

= -√[(1 + (-4/5)) / 2]

= -√[(5 - 4)/10]

= -√[1/10]

Rationalizing the denominator, we get

= -√10/10

ii)

tan (a/2) = √[(1 - cos a) / (1 + cos a)]

= √[(1 - (-4/5)) / (1 + (-4/5))]

= √[(9/5)) / (1/5)]

= √[(9/5) x (5/1)]

= √9

= 3

Example 6 :

2 cosec x cos² (x/2) = sin x / (1 - cos x)

Solution :

L.H.S :

= 2 cosec x cos² (x/2)

= 2 cosec x · (1 + cos x)/2

= 2 (1/sin x) (1 + cos x)/2

= (1 + cos x)/sin x

Multiplying by the conjugate of the numerator, we get

= (1 + cos x)/sin x ·[(1 - cos x) / (1 - cos x)]

= 1² - cos²x / sin x(1 - cos x)

= sin²x / sin x(1 - cos x)

= sin x / (1 - cos x)

Hence it is proved.

Example 7 :

Use the figure to find the exact value of each of the following.

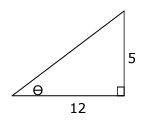
i) cos (θ/2)     ii)  sin (θ/2)     iii)  tan (θ/2)

iv)  sec (θ/2)     v)  csc (θ/2)     vi)  cot (θ/2)

vii)  2 sin (θ/2) cos (θ/2)     viii)  2 cos (θ/2) tan (θ/2)

Solution :

i) cos (θ/2)

Using formula for cos (θ/2),

 = √[(1+cosθ)/2]

From the triangle given above, 

(Hypotenuse)² = 12² + 5²

(Hypotenuse)² = 144 + 25

Hypotenuse = √169 ==> 13

cos θ = Adjacent side / hypotenuse

cos θ = 12/13

 = √[(1 + (12/13))/2]

 = √(25/26)

 = 5/√26

Rationalizing the denominator, we get

= 5√26/26

ii)  sin (θ/2)

Using formula for sin (θ/2),

 = √[(1-cosθ)/2]

 = √[(1 - (12/13))/2]

 = √(1/26)

 = 1/√26

Rationalizing the denominator, we get

= √26/26

iii)  tan (θ/2)

Here tan (θ/2) = sin (θ/2) / cos (θ/2)

= (√26/26) / (5√26/26)

= (√26/26) · (26/5√26)

= 1/5

iv)  sec (θ/2)

sec (θ/2) = 1/cos (θ/2) 

= 1/(5√26/26)

= 26/5√26

Rationalizing the denominator, we get

= √26/5

v)  csc (θ/2)

csc (θ/2) = 1/sin (θ/2)

= 1/(√26/26)

= 26/√26

Rationalizing the denominator, we get

= √26

vi)  cot (θ/2)

cot (θ/2) = 1/tan (θ/2)

= 1/(1/5)

= 5

vii)  2 sin (θ/2) cos (θ/2)

From the above calculation, we know the values of sin (θ/2) and cos (θ/2). Applying these values, we get

= 2 (√26/26)· (5√26/26)

= 2 (5·26) / (26 · 26)

= (2 · 5)/26

= 5/13

viii)  2 cos (θ/2) tan (θ/2)

From the above calculation, we know the values of cos (θ/2) and tan (θ/2). Applying these values, we get

cos (θ/2) = 5√26/26

tan (θ/2) = 1/5

= 2(5√26/26) (1/5)

= √26/13

Example 8 :

Using half angle identities to determine the exact values of each function.

i) cos π/12    ii)  tan (3π/8)

Solution :

i) cos π/12

ii)  tan (3π/8)

cos (3π/4) = cos (π - (π/4))

= - cos (π/4)

= - √2/2

sin (3π/4) = sin (π - (π/4))

= sin (π/4)

= √2/2

Applying these values, we get

= (1+√2/2) / (√2/2)

= (2 + √2)/2 · (2/√2)

= (2 + √2) / √2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.