HALF ANGLE IDENTITIES IN TRIGONOMETRY
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
sin A = 2 sin (A/2) cos (A/2)
cos A = cos2 (A/2) - sin2(A/2)
tan A = 2 tan (A/2)/[1-tan2(A/2)]
cos A = 1 - 2sin2(A/2)
cos A = 2cos²(A/2) - 1
sin A = 2 tan (A/2)/[1+tan2(A/2)]
cos A = [1-tan2(A/2)]/[1+tan2 (A/2)]
sin2(A/2) = (1-cos A)/2
cos2(A/2) = (1+cos A)/2
tan2(A/2) = (1-cos A)/(1+cos A)
Example 1 :
Using half angle find the value of sin 15°
Solution :
We may write, 15° = 30°/2
So,
sin 15° = sin (30°/2)
We know that,
sin2A/2 = (1-cosA)/2
sin (A/2) = √ (1-cosA)/2
sin (30°/2) = √[(1-cos 30)/2]
= √[(1-√3/2)/2]
= √[(2-√3)/4]
= √(2-√3)/2
Example 2 :
Using half angle formula find the value of tan 15°
Solution :
15° = 30°/2
So, tan 15° = tan 30°/2
tan²(A/2) = (1-cos A)/(1+cos A)
tan(A/2) = √(1-cos A)/(1+cos A)
tan 30°/2 = √[(1-cos 30°)/(1+cos 30°)]
= √[(1-√3/2)/(1+√3/2)]
= √[( 2-√3 )/2] x [2/(2+√3)]
= √(2-√3)/(2+√3)
Rationalizing the denominator,
= √[(2-√3)2/(22 - (√3)2]
= √[(2²+(√3)² - 2(2)(√3) /(2² - (√3)²]
= √[(2²+(√3)² - 2(2)(√3) /(4-3]
= √[(2-√3)² /1]
= √[(2-√3)2
= 2-√3
So, the value of tan 15° is 2-√3.
Example 3 :
Using half angle find the value of cos 15°
Solution :
15° = 30°/2
So, cos 15° = cos 30°/2
cos²A/2 = (1+cos A)/2
cos (A/2) = √(1+cos A)/2
cos 30°/2 = √[(1+cos 30)/2]
= √[(1+√3/2)/2]
= √[(2+√3)/4]
= √(2+√3)/2
Example 4 :
Find the exact value of cos 105°
Solution :
105° = 210°/2
From cos 2A = 2cos2 A - 1,
cos2 A = (1 + cos 2A) / 2
cos A = √[(1 + cos 2A) / 2]
Dividing the angle by 2, we get
cos (A/2) = √[(1 + cos A) / 2]
cos (210/2) = √[(1 + cos 210) / 2] ----(1)
Angle 210 lies in 3rd quadrant,
cos 210 = cos (180 + 30)
= -cos 30
= -√3/2
By applying the value of cos 210 in (1), we get
= √[(1 + (-√3/2)) / 2]
= √[(2 - √3)/4]
= √(2 - √3)/2
Example 5 :
If sin a = -3/5 and 180 < a < 270, find the exact value of
i) cos (a/2) ii) tan (a/2)
Solution :
sin a = -3/5
From sin2 a + cos2 a = 1
cos2 a = 1 - sin2 a
cos a = √(1 - sin2 a)
= √(1 - (-3/5)2)
= √(1 - (9/25))
= √(25 - 9)/25
= √(16/25)
Since the angle a lies in 3rd quadrant,
cos a = -4/5
cos (a/2) = -√[(1 + cos a) / 2]
= -√[(1 + (-4/5)) / 2]
= -√[(5 - 4)/10]
= -√[1/10]
Rationalizing the denominator, we get
= -√10/10
ii)
tan (a/2) = √[(1 - cos a) / (1 + cos a)]
= √[(1 - (-4/5)) / (1 + (-4/5))]
= √[(9/5)) / (1/5)]
= √[(9/5) x (5/1)]
= √9
= 3
Example 6 :
2 cosec x cos2 (x/2) = sin x / (1 - cos x)
Solution :
L.H.S :
= 2 cosec x cos2 (x/2)
= 2 cosec x · (1 + cos x)/2
= 2 (1/sin x) (1 + cos x)/2
= (1 + cos x)/sin x
Multiplying by the conjugate of the numerator, we get
= (1 + cos x)/sin x ·[(1 - cos x) / (1 - cos x)]
= 12 - cos2x / sin x(1 - cos x)
= sin2x / sin x(1 - cos x)
= sin x / (1 - cos x)
Hence it is proved.
Example 7 :
Use the figure to find the exact value of each of the following.
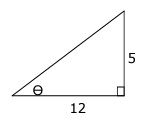
i) cos (θ/2) ii) sin (θ/2) iii) tan (θ/2)
iv) sec (θ/2) v) csc (θ/2) vi) cot (θ/2)
vii) 2 sin (θ/2) cos (θ/2) viii) 2 cos (θ/2) tan (θ/2)
Solution :
i) cos (θ/2)
Using formula for cos (θ/2),
= √[(1+cosθ)/2]
From the triangle given above,
(Hypotenuse)2 = 122 + 52
(Hypotenuse)2 = 144 + 25
Hypotenuse = √169 ==> 13
cos θ = Adjacent side / hypotenuse
cos θ = 12/13
= √[(1 + (12/13))/2]
= √(25/26)
= 5/√26
Rationalizing the denominator, we get
= 5√26/26
ii) sin (θ/2)
Using formula for sin (θ/2),
= √[(1-cosθ)/2]
= √[(1 - (12/13))/2]
= √(1/26)
= 1/√26
Rationalizing the denominator, we get
= √26/26
iii) tan (θ/2)
Here tan (θ/2) = sin (θ/2) / cos (θ/2)
= (√26/26) / (5√26/26)
= (√26/26) · (26/5√26)
= 1/5
iv) sec (θ/2)
sec (θ/2) = 1/cos (θ/2)
= 1/(5√26/26)
= 26/5√26
Rationalizing the denominator, we get
= √26/5
v) csc (θ/2)
csc (θ/2) = 1/sin (θ/2)
= 1/(√26/26)
= 26/√26
Rationalizing the denominator, we get
= √26
vi) cot (θ/2)
cot (θ/2) = 1/tan (θ/2)
= 1/(1/5)
= 5
vii) 2 sin (θ/2) cos (θ/2)
From the above calculation, we know the values of sin (θ/2) and cos (θ/2). Applying these values, we get
= 2 (√26/26)· (5√26/26)
= 2 (5·26) / (26 · 26)
= (2 · 5)/26
= 5/13
viii) 2 cos (θ/2) tan (θ/2)
From the above calculation, we know the values of cos (θ/2) and tan (θ/2). Applying these values, we get
cos (θ/2) = 5√26/26
tan (θ/2) = 1/5
= 2(5√26/26) (1/5)
= √26/13
Example 8 :
Using half angle identities to determine the exact values of each function.
i) cos π/12 ii) tan (3π/8)
Solution :
i) cos π/12
ii) tan (3π/8)
cos (3π/4) = cos (π - (π/4))
= - cos (π/4)
= - √2/2
sin (3π/4) = sin (π - (π/4))
= sin (π/4)
= √2/2
Applying these values, we get
= (1+√2/2) / (√2/2)
= (2 + √2)/2 · (2/√2)
= (2 + √2) / √2
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus BC Problems with Solutions
Dec 20, 25 10:51 AM
AP Calculus BC Problems with Solutions -
AP Precalculus Problems and Solutions (Part - 1)
Dec 20, 25 10:49 AM
AP Precalculus Problems and Solutions (Part - 1) -
AP Calculus AB Problems with Solutions (Part - 1)
Dec 20, 25 10:49 AM
AP Calculus AB Problems with Solutions (Part - 1)