GRAPHING GREATEST INTEGER FUNCTION WORKSHEET

Question 1 :

[4.5] = ?

Question 2 :

[5.6] = ?

Question 3 :

[-2.3] = ?

Question 4 :

[-5.6] = ?

Question 5 :

[-7.8] = ?

Question 6 :

Graph :

y = [x - 2]

Question 7 :

Graph :

y = [x] + 3

Question 8 :

Graph :

y = [x + 1] + 2

Answers

1. Answer :

To have value of [4.5], we have to mark 4.5 on the number line as shown below.

Pick the nearest integer on the left side of 4.5.

That is 4.

[4.5] = 4

2. Answer :

To have value of [5.6], we have to mark 5.6 on the number line as shown below.

Pick the nearest integer on the left side of 5.6.

That is 5.

[5.6] = 5

3. Answer :

To have value of [-2.3], we have to mark -2.3 on the number line as show below below.

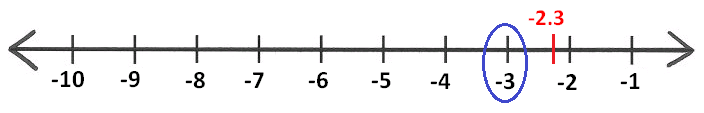
Pick the nearest integer on the left side of -2.3.

That is -3.

[-2.3] = -3

4. Answer :

To have value of [-5.6], we have to mark -5.6 on the number line as shown below.

Pick the nearest integer on the left side of -5.6.

That is -6.

[-5.6] = -6

5. Answer :

To have value of  [-7.8], we have to mark -7.8 on the number line as shown below.

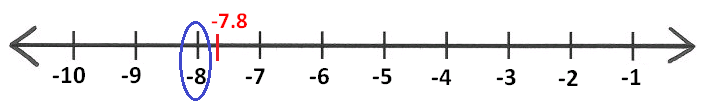
Pick the nearest integer on the left side of -7.8.

That is -8.

[-7.8] = -8

6. Answer :

y = [x - 2]

The given function is in the form of y - a = [x - b].

Let y = 0 and x - 2 = 0. Then, y = 0 and x = 2.

From y = 0, there is no vertical shift.

From x = 2, we have an horizontal shift of 2 units to the right.

So each point of the parent function to be shifted 2 units to the right.

If we do the above transformation, we will have a graph as given below.

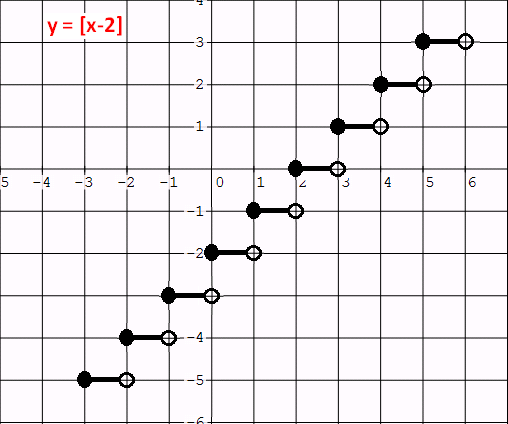
7. Answer :

y = [x] + 3

If we write the given function in the form of

y - a = [x - b],

we will have y - 3 = [x].

Let y - 3 = 0 and x = 0. Then, y = 3 and x = 2.

From y = 3, we have a vertical shift of 3 units up.

From x = 0, there is no horizontal shift.

So each point of the parent function to be shifted 3 units up.

If we do the above transformation, we will have a graph as given below.

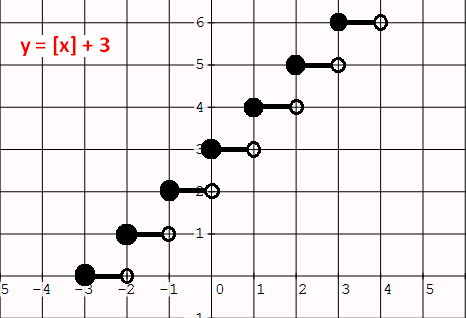
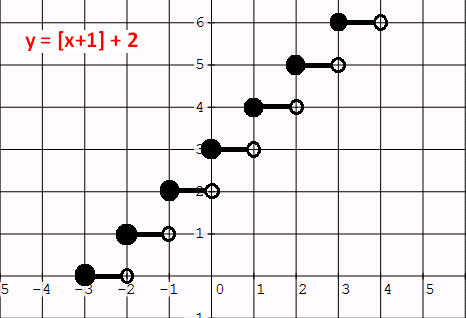
8. Answer :

y = [x + 1] + 2

If we write the given function in the form of

y - a = [x - b],

we will have y - 2 = [x + 1].

Let y - 2 = 0 and x + 1 = 0. Then y = 2 and x = -1.

From y = 2, we have a vertical shift of 2 units up.

From x = - 1, we have an horizontal shift of 1 unit to the left.

So each point of the parent function to be shifted 2 units up and 1 unit to the left.

If we do the above transformations, we will have a graph as given below.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.