GREATEST COMMON FACTOR WORKSHEET

Detailed Answer Key

1. Answer :

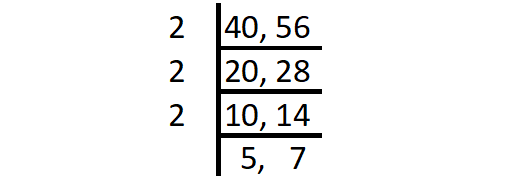
The product of common factors of 40 and 56 is

=  2 x 2 x 2

=  8

So, GCF (40, 56) = 8.

2. Answer :

Find the factors of 18, 24 and 30 by tree method. 

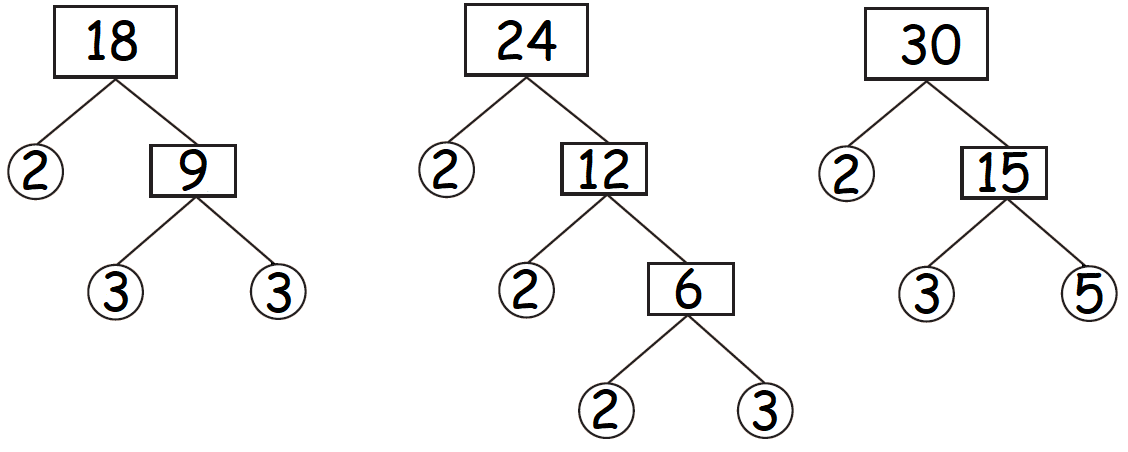
Let us find the factors of 18, 24 and 30 (use of  divisibility test rules will also help).

The factors of 18 are 1, 2, 3, 6, 9 and 18.

The factors of 24 are  1, 2, 3, 4, 6, 8, 12 and 24.

The factors of 30 are  1, 2, 3, 5, 6, 10, 15 and 30.

The factors that are common to all the three given numbers are 1, 2, 3 and 6 of which 6 is the highest.

So, GCF (18, 24, 30) = 6.

Note :

1 is a trivial factor of all numbers.

3. Answer :

Write the prime factors of 36 and 48. 

36  =  2 x 2 x 3 x 3 

48  =  2 x 2 x 2 x 2 x 3

The prime factors that are common to 36 and 48 are

2, 2 and 3

Product of common prime factors :

=  2 x 2 x 3

=  12

So, GCF (36, 48) = 12.

4. Answer :

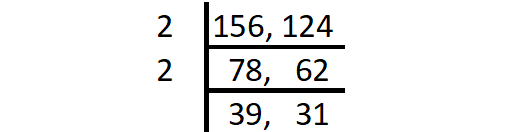
The product of common factors of 156 and 124 is

=  2 x 2

=  4

So, GCF (156, 124) = 4.

5. Answer :

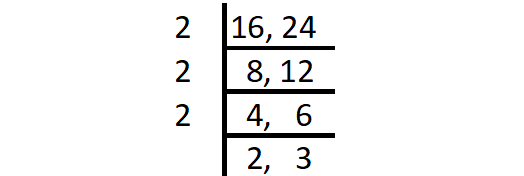
The product of common factors of 16 and 24 is

=  2 x 2 x 2

=  8

So, GCF (16, 24) = 8.

6. Answer :

The product of common factors of 84 and 120 is

=  2 x 2 x 3

=  12

So, GCF (84, 120) = 12.

7. Answer :

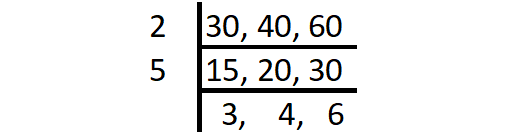
The product of common factors of 30, 40 and 60 is

=  2 x 5

=  10

So, GCF (30, 40, 60) = 10.

8. Answer : 

In the given two numbers 0.45 and 0.75, we find equal number of digits after the decimal point. That is, two digits. 

To get rid of the decimal point, we have to multiply each number by 100.

0.45 x 100  =  45

0.75 x 100  =  75

Find the greatest common factor 45 and 75 using prime factorization method.

Write the prime factors of 45 and 75 as shown below. 

45  =  3 x 3 x 5 

75  =  3 x 5 x 5

The prime factors that are common to 45 and 75 are

3 and 5

Product of common prime factors :

=  3 x 5

=  15

GCF (45, 75) = 15.

Divide the GCF (15) by 100.

15 / 100  =  0.15

So, the greatest common factor of 0.45 and 0.75 is

0.15

9. Answer : 

In the given two numbers 0.48 and 0.6, we find more number of digits after the decimal point in 0.48. That is, two digits. 

(To get rid of the decimal point, always we have to multiply both the numbers by the same powers of 10)

To get rid of the decimal point, we have to multiply each number by 100.

0.48 x 100  =  48

0.6 x 100  =  60

Find the greatest common factor 48 and 60 using prime factorization method.

Write the prime factors of 48 and 60 as shown below. 

48  =  2 x 2 x 2 x 2 x 3 

60  =  2 x 2 x 3 x 5

The prime factors that are common to 48 and 60 are

2, 2 and 3

Product of common prime factors :

=  2 x 2 x 3

=  12

GCF (48, 60) = 12.

Divide the GCF (12) by 100.

12 / 100  =  0.12

So, the greatest common factor of 0.48 and 0.6 is

0.12

10. Answer :

Formula to find the greatest common factor (GCF) of fractions :

=  GCF of Numerators / LCM of Denominators

*GCF -----> greatest common factor

*LCM -----> least common multiple

GCF of numerators (3, 7)  =  1

LCM of denominators (5, 10)  =  10

Greatest common factor of 3/5 and 7/10 is 

=  GCF (3, 7) / LCM (5, 10)

=  1/10

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.