GREATEST COMMON FACTOR WORD PROBLEMS

Problem 1 :

Find the greatest possible length that can be used to measure exactly the lengths 84 feet, 98 feet and 126 feet.

Solution :

The greatest possible length that can be used to measure the given lengths is the greatest common factor of 84, 63 and 97.

Find the greatest common factor of 84, 98 and 126.

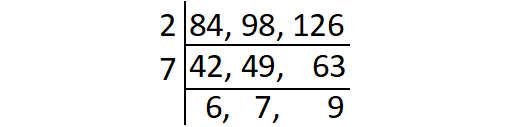
Product of common factors of 84, 98 and 126 is

= 2 x 7

= 14

GCF (84, 98, 126) = 14.

The greatest possible length that can be used to measure the given lengths is 14 feet.

Problem 2 :

A warehouse has three shelves that can hold 8, 12, or 16 skateboards. Each shelf has sections holding the same number of skateboards. What is the greatest number of skateboards that can be put in a section? Explain

Solution :

Write the factors of 8, 12 and 16.

8 = 1, 2, 4, 8

12 = 1, 2, 3, 4, 6, 12

16 = 1, 2, 4, 8, 16

The greatest common factor of 8, 12 and 16 is 4.

So, the greatest number of skateboards can be put in a section is 4.

Problem 3 :

Lily has 15 oranges, 9 peaches, and 18 pears. She wants to put all of the fruit into decorative baskets. Each basket must have the same number of pieces of fruit in it. Without mixing fruits, what is the greatest number of pieces of fruit Lily can put in each basket? Explain.

Solution :

Write the factors of 15, 9 and 18.

15 = 1, 2, 3, 5, 15

9 = 1, 3, 9

18 = 1, 2, 3, 6, 9, 18

The greatest common factor of 15, 9 and 18 is 3.

So, the greatest number of pieces of fruit Lily can put in each basket is 3.

Problem 4 :

A store has 120 lbs and 250 lbs of two kinds of meat. The store wants to sell the meat by filling the two kinds in boxes of equal volumes and no meat left over. Find the greatest volume of such a box.

Solution :

The given two quantities 120 and 250 can be divided by 2, 5, 10,... exactly. That is, both kinds of meat can be sold in boxes of equal volume of 2, 5, 10,...

But, the volume of meat filled in boxes must be greatest.

So, we have to find the largest number which exactly divides 120 and 250. That is the highest common factor (HCF) of 120 and 250.

HCF (120, 250) = 10

The 1^st kind 120 lbs is sold in 12 boxes of volume 10 lbs in each box.

The 2^nd kind 250 lbs is sold in 25 boxes of volume 10 lbs in each box.

Hence, the greatest volume of the box is 10 lbs.

Problem 5 :

Two numbers are in the ratio 2 : 3. If the second number is 27, find their greatest common factor.

Solution :

Because the two numbers are in the ratio 2 : 3, the numbers can be assumed as 2x and 3x.

Find the greatest common multiple of 2x and 3x.

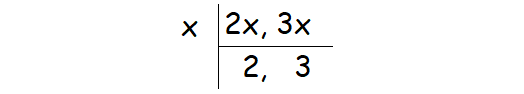
The common factor of 2x and 3x is x.

Greatest common factor (2x, 3x) = x

But, it is given that the second number is 27.

Then,

3x = 27

Divide each side by 3.

x = 9

So, the greatest factor of the two numbers is 9.

Problem 6 :

Two numbers are in the ratio 3 : 5 and their greatest common factor is 18. Find the numbers.

Solution :

Because the two numbers are in the ratio 3 : 5, the numbers can be assumed as 3x and 5x.

Greatest common factor (3x, 5x) = x

But, it is given that the greatest common factor of the two numbers is 18.

Then,

x = 18

Substitute x = 18 in 3x and 5x.

3x = 3(18) = 54

5x = 5(18) = 90

So, the two numbers are 54 and 90.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.