GRAPHING WITH RATIOS

Problem 1 :

• You are skateboarding at a pace of 30 meters every 5 seconds.
• Your friend is in-line skating at a pace of 9 meters every 2 seconds.

Graph each ratio relationship in the same coordinate plane. Who is faster?

Solution :

Distance covered = 30 meters 

Time taken = 5 seconds

Distance covered in 1 second = 30/5

= 6 meters

Let x be the time taken in seconds and y be the distance in meters.

y = 6x

The points are (1, 6) (2, 12) (3, 18) (4, 24) and (5, 30)

Distance covered = 9 meters 

Time taken = 2 seconds

Distance covered in 1 second = 9/2

= 4.5 meters

Let x be the time taken in seconds and y be the distance in meters.

y = 4.5x

The points are (1, 4.5) (2, 9) (3, 13.5) (4, 18) and (5, 22.5)

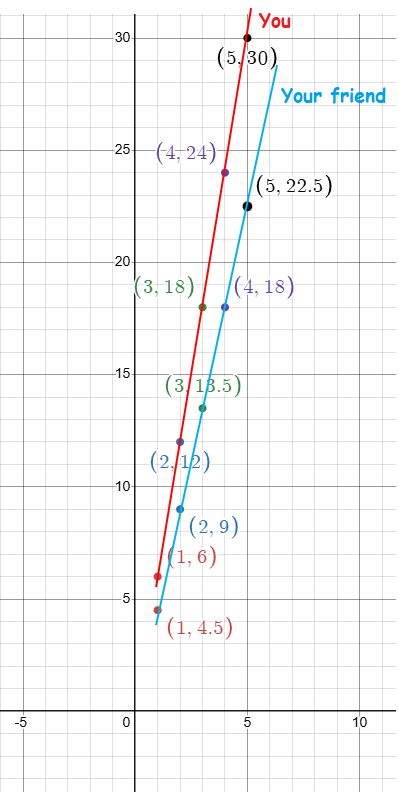
You are faster.

Problem 2 :

You buy 2.5 pounds of pumpkin seeds and 2.5 pounds of sunflower seeds. Use a graph to find your total cost. Then use the graph to determine how much more you pay for pumpkin seeds than for sunflower seeds.

Solution :

From the picture given picture above,

Cost of pumpkin seeds = $6.50 per pound

Let x be the number of pounds and y be the total cost.

y = 6.50x

The points are (1, 6.50) (2, 13) (3, 19.50) (4, 26) and (5, 32.5)

Cost of sunflower seeds = $4 per pound

Let x be the number of pounds and y be the total cost.

y = 4x

So, the points are (1, 4) (2, 8) (3, 12) (4, 16) and (5, 20)

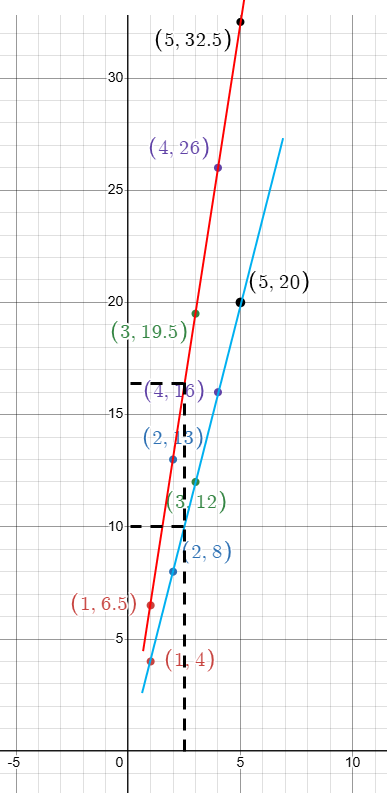
From the graph,

• Cost of pumpkin seeds for 2.5 pounds = $16.25
• Cost of sunflower seeds for 2.5 pounds = $10

From the calculation,

Cost of pumpkin seeds for 2.5 pounds 

= 6.5(2.5) ==> $16.25

Cost of sunflower seeds for 2.5 pounds

= 4(2.5) ==> $10

Find the missing values in the ratio table. Then write the equivalent ratios.

Problem 3 :

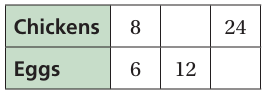
Solution :

Chikens and eggs is in the ratio

= 8 : 6

Simplifying it, we get

= 4 : 3

Second column :

Let x be the unknwon.

x : 12 = 4 : 3

x/12 = 4/3

3x = 4(12)

x = 48/3

x = 16

Third column :

Let y be the unknown,

24 : y = 4 : 3

24/y = 4/3

3(24) = 4y

y = 3(24)/4

y = 3(6)

y = 18

Problem 4 :

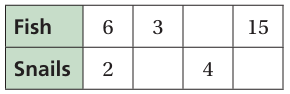
Solution :

Fishes and snails is in the ratio

= 6 : 2

Simplifying it, we get

= 3 : 1

Second column :

Let y be the unknwon.

3 : y = 3 : 1

3/y = 3/1

3 = 3y

y = 1

Third column :

Let x be the unknown,

x : 4 = 3 : 1

x/4 = 3/1

x = 4(3)

x = 12

Fourth column :

Let y be the unknown,

15 : y = 3 : 1

15/y = 3/1

15 = 3y

y = 15/3

y = 5

Problem 5 :

Just by looking at the graph, determine who earns a greater hourly wage. Explain.

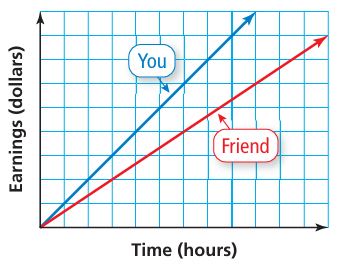
Solution :

Considering the blue line and red line, the slope of the blue line is greater then you earn more.

Problem 6 :

Your freezer produces 8 ice cubes every 2 hours. Your friend’s freezer produces 24 ice cubes every 5 hours. Graph each ratio relationship in the same coordinate plane. Whose freezer produces ice faster?

Solution :

Your freezer :

8 ice cubes for every 2 hours

In 1 hour, number of ice cubes produced = 8/2

= 4 ice cubes

Your friend's freezer :

24 ice cubes for every 5 hours

In 1 hour, number of ice cubes produced = 24/5

= 4.8 ice cubes

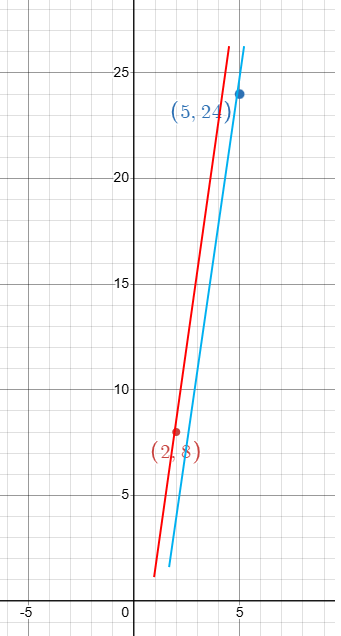
The blue line is more steeper than red line and comparing the calculation 4.8 is greater than 4.

Then, your friend's freezer produces faster.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.