SOLVE A SYSTEM OF EQUATIONS BY GRAPHING
The following steps will be useful to solve system of linear equations in two variables.
Step 1 :
Write the given linear equations in slope-intercept form.
Step 2 :
Graph both the equations on a xy-plane.
Step 3 :
Locate the point of intersection of the two lines.
At the point of intersection, x-coordinate will represent the value of x and y-coordinate will represent the value of y of the given system of linear equations.
Solve the following systems of linear equations by graphing :
Example 1 :
y = x – 3
y = 3
Solution :
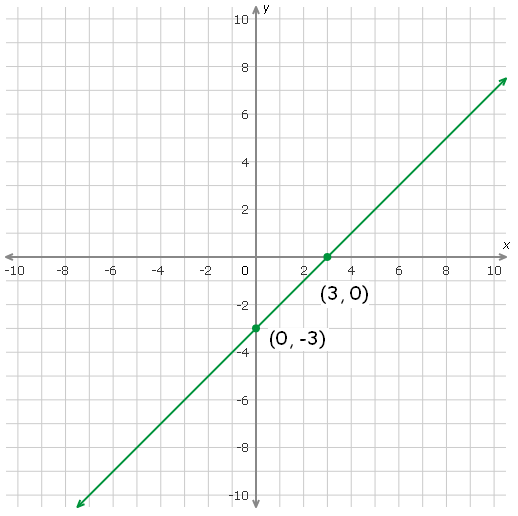
y = x – 3 :
The given equation is in slope-intercept form. Substitute some random values for x and find their corresponding values of y.
When x = 0,
y = 0 - 3
= -3
(0, -3)
When x = 3,
y = 3 - 3
= 0
(3, 0)
Plot the points (0, -3), and (3, 0) on a xy-plane and connect them.
y = 3 :
This is the equation of a line parallel to x-axis through the value 3 on y-axis.
So, graph a straight parallel to x-axis through the value 3 on y-axis.
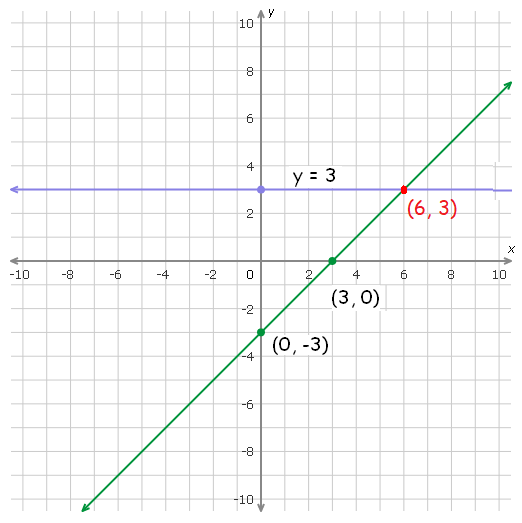
In the graph above, the two lines intersect at (6, 3).
So,
x = 6 and y = 3
Example 2 :
2x + y - 2 = 0
5x + y + 1 = 0
Solution :
2x + y - 2 = 0 :
The given equation is not in slope-intercept form. Write the given equation is in slope intercept form.
2x + y - 2 = 0
Subtract 2x from both sides.
y - 2 = -2x
Add 2 to both sides.
y = -2x + 2
Now the equation is in slope-intercept form. Substitute some random values for x and find their corresponding values of y.
When x = -1,
y = -2(-1) + 2
= 2 + 2
= 4
(-1, 4)
When x = 0,
y = -2(0) + 2
= 0 + 2
= 2
(0, 2)
Plot the points (-1, 4), and (0, 2) on a xy-plane and connect them.
5x + y + 1 = 0 :
The given equation is not in slope-intercept form. Write the given equation is in slope intercept form.
5x + y + 1 = 0
Subtract 5x and 1 from both sides.
y = -5x - 1
Now the equation is in slope-intercept form. Substitute some random values for x and find their corresponding values of y.
When x = -1,
y = -5(-1) - 1
= 5 - 1
= 4
(-1, 4)
When x = 0,
y = -5(0) - 1
= 0 - 1
= -1
(0, -1)
Plot the points (-1, 4), and (0, -1) on a xy-plane and connect them.
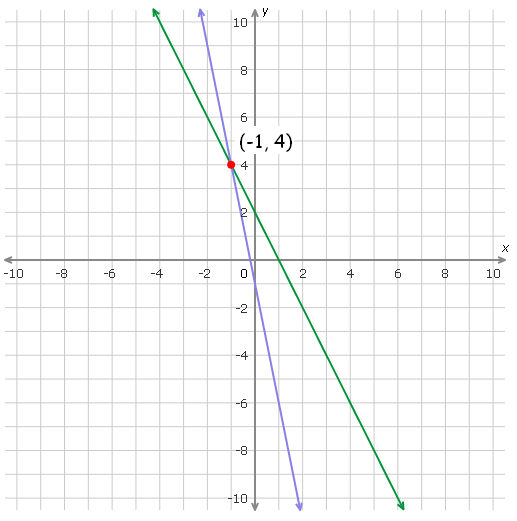
In the graph above, the two lines intersect at (-1, 4).
So,
x = -1 and y = 4
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Precalculus Problems and Solutions (Part - 15)
May 24, 25 02:40 AM
Precalculus Problems and Solutions (Part - 15) -
Digital SAT Math Problems and Solutions (Part - 168)
May 23, 25 07:42 PM
Digital SAT Math Problems and Solutions (Part - 168) -
Precalculus Problems and Solutions (Part - 14)
May 23, 25 07:15 PM
Precalculus Problems and Solutions (Part - 14)