GRAPHING QUADRATIC EQUATION AND FIND THE NATURE OF ROOTS

Solved Questions 

Graph the following quadratic equations and state their nature of solutions.

Question 1 :

x² - 6x + 9 = 0

Solution :

Draw the graph for the function y = x² - 6x + 9.

Let us substitute some random values for x and find the corresponding values of y.

Points to be plotted :

(-3, 0), (-2, 1), (-1, 4), (0, 9), (1, 4), (2, 1), (3, 0), (4, 1)

Formula To find the x-coordinate of the vertex of the parabola, we may use the formula x = -b/2a.

x = -(-6)/2(1)  =  6/2  =  3

By applying x = 3, we get the value of y.

y = 3² - 6(3) + 9 

y = 9 - 18 + 9

y = 0

Vertex (3, 0)

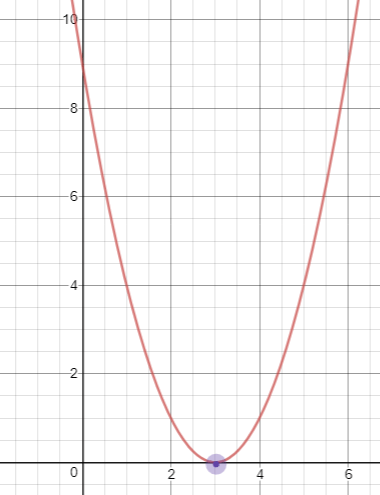
The graph of the given parabola intersect the x-axis at the one point. Hence it has real and equal roots.

Question 2 :

Graph the following quadratic equations and state their nature of solutions.

(2x - 3)(x + 2) = 0

Solution :

(2x - 3)(x + 2) = 0

2x² + 4x - 3x - 6 = 0

2x² + x - 6 = 0

Let us give some random values of x and find the values of y.

y = 2x² + x - 6 :

Points to be plotted :

(-4, 22) (-3, 9) (-2, 0) (-1, -5) (0, -6) (1, -4) (2, 4) (3, 15) (4, 30)

To find the x-coordinate of the vertex of the parabola, we may use the formula x = -b/2a.

x = -1/2(2) = 1/4

By applying x = 1/4, we get the value of y.

y = 2(1/4)² + (1/4) - 6

y = 2(1/16) + (1/4) - 6

y = -45/8

Vertex (1/4, -45/8).

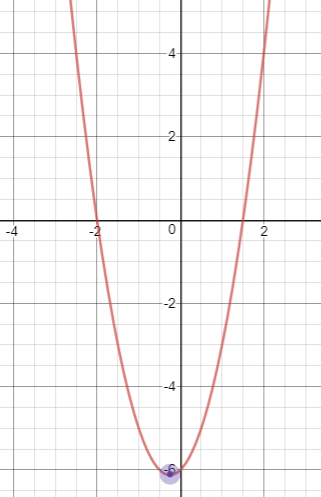
The graph of the given parabola intersects the x-axis at two points. Hence it has two real and unequal roots.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.