GRAPHING POLAR EQUATIONS

Example 1 :

Graph each of the following polar equations. Convert to rectangular coordinates, if possible.

(a)  r  =  3   (b) θ  =  π/6    (c) r sinθ  =  2    (d)  r  =  sec θ

Solution :

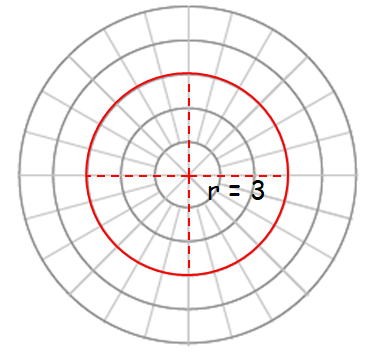
(a)  r  =  3

r is the directed distance from origin.

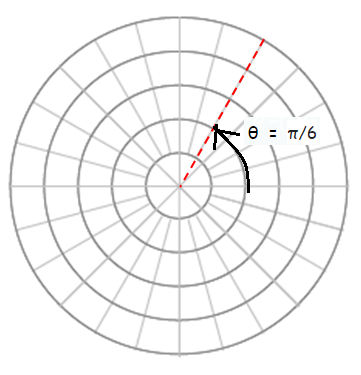
(b) θ  =  π/6

Angle formed in the positive along x axis.

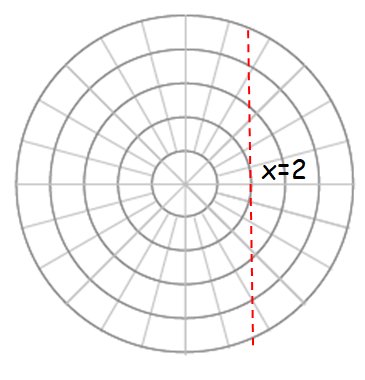
(c) r sinθ  =  2

Since r sinθ  =  x

By replacing r sinθ by x, we get

x  =  2

It is a straight line which is at 2 units distance from the origin.

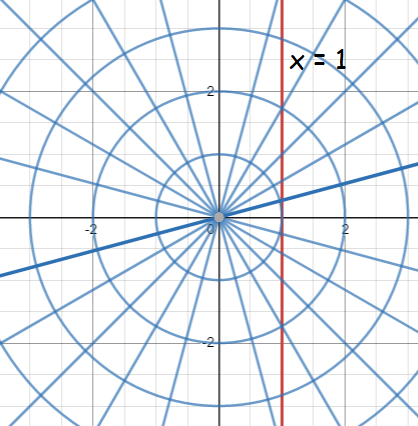
(d)  r  =  sec θ

r/sec θ  =  1

r cos θ  =  1

x  =  1

Example 2 :

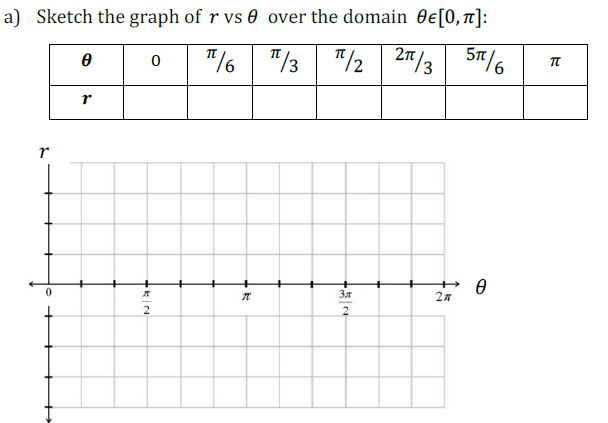
Consider the equation r(θ)  =  2 sinθ 

Solution :

(a)

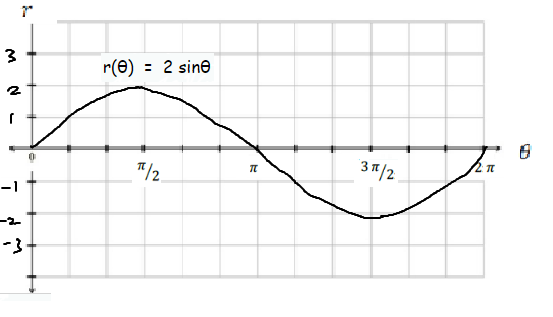
(b)  Sketch the equation again but this time in terms of y vs x.

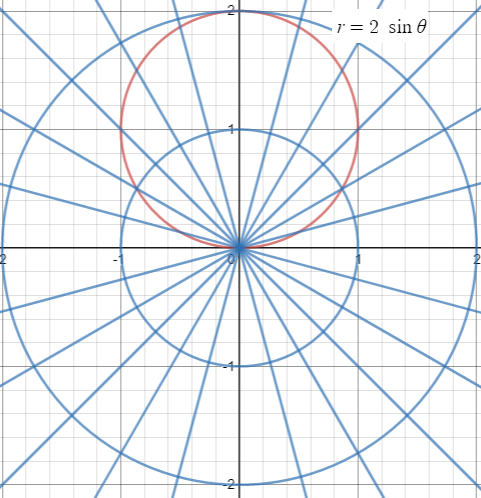
(c)  If the domain is changed as [0, 2π], the graph will be same.

Example 3 :

Graph each polar equation then convert it into rectangular form.

(a)  1  =  r sin θ    (b)  r  =  -3/cos θ

Solution :

r  =  1/sin θ

If θ  =  30, r  =  2

If θ  =  45, r  =  √2

If θ  =  60, r  =  2/√3

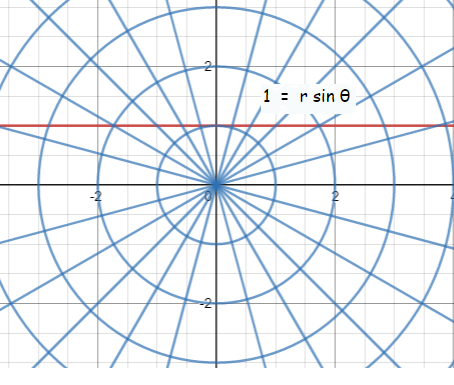
Converting the given into rectangular form :

Polar Equation  :

1  =  r sinθ

r sinθ  =  x

Rectangular form :

y  =  1

(b)  r  =  -3/cos θ

Solution :

r  =  -3/cos θ

If θ  =  0, r  =  -3

If θ  =  30, r  =  -2√3

If θ  =  45, r  =  -3√2

If θ  =  60, r  =  -6

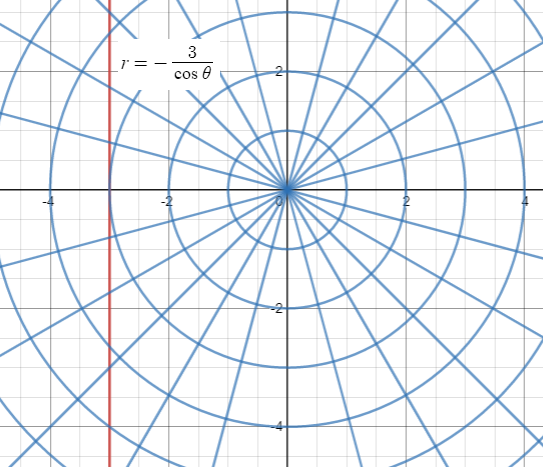
Converting the given into rectangular form :

Polar Equation  :

r  =  -3/cosθ

r cos  =  -3

Rectangular form :

x  =  -3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.