GRAPHING LINEAR INEQUALITIES IN TWO VARIABLES

A linear inequality in x and y is an inequality that can be written in one of the following forms.

ax + by < c

ax + by ≤ c

ax + by > c

ax + by ≥ c

An ordered pair (a, b) is a solution to a linear inequality in x and y if the inequality is true when a and b are substituted for x and y, respectively.

Graph the following inequalities :

Example 1 :

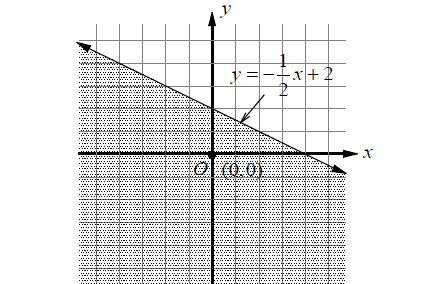
2y + x ≤ 4

Solution :

The corresponding equation is 2y + x = 4.

Write the equation in slope-intercept form.

y = -(½)x + 2

Graph the line that has a slope of -½ and a y-intercept of 2. Since the inequality sign is ≤, the boundary should be drawn as a solid line. Select a point in one of the half planes and test it.

Let's check the given inequality with (0, 0).

2y + x ≤ 4

2(0) + 0 ≤ 4

0 ≤ 4

Since the statement is true, shade the half plane containing the origin.

Example 2 :

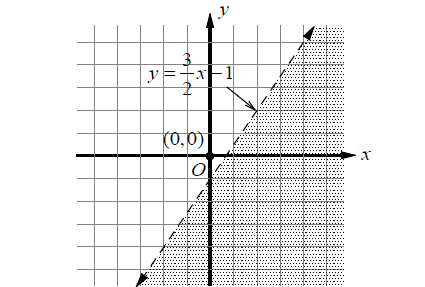
3x - 2y > 2

Solution :

The corresponding equation is 3x - 2y = 2.

Write the equation in slope-intercept form.

y = (³⁄₂)x - 1

Graph the line that has a slope of ³⁄₂ and a y-intercept of -1. Since the inequality sign is >, the boundary should be drawn as a dashed line. Select a point in one of the half planes and test it.

Let's check the given inequality with (0, 0).

3x - 2y > 2

3(0) - 2(0) > 2

0 > 2

Since the statement is false, shade the other half plane not containing the origin.

Solved Problems

Problem 1 :

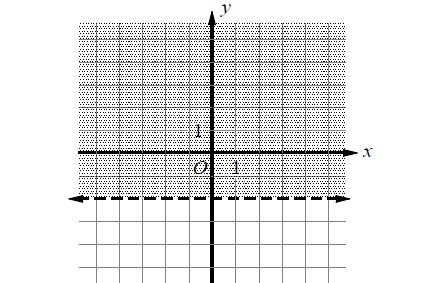
Which of the following inequalities represents the graph above?

(A)  x > -2

(B)  x < -2

(C)  y > -2

(D)  y < -2

Solution :

The equation of the boundary line is y = -2. Any point above that horizontal has a y-coordinate that satisfies

y > -2

Since the boundary line is drawn as a dashed line, the inequality should not include an equal sign.

Therefore, the correct answer is option (C).

Problem 2 :

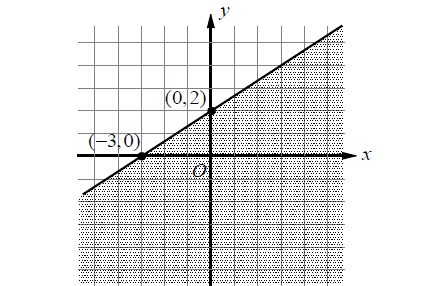
Which of the following inequalities represents the graph above?

(A)  2y - 3x ≥ 6

(B)  2y - 3x ≤ 6

(C)  3y - 2x ≥ 6

(D)  3y - 2x ≤ 6

Solution :

The slope-intercept form of the boundary line is

y = (⅔)x + 2

The standard form of the line is

3y - 2x = 6

Since the boundary line is drawn as a solid line, the inequality should include an equal sign. Select a point in the plane which is not on the boundary line and test the inequalities in the answer choices. Let’s use (0, 0).

In option (C),

3y - 2x ≥ 6

3(0) - 2(0) ≥ 6

0 - 0 ≥ 6

0 ≥ 6 (false)

In option (D),

3y - 2x ≤ 6

3(0) - 2(0) ≤ 6

0 - 0 ≤ 6

0 ≤ 6 (true)

Therefore, the correct answer is option (D).

Problem 3 :

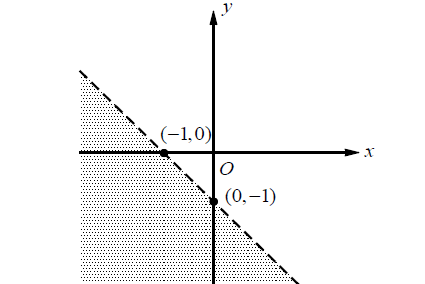
Which of the following inequalities represents the graph above?

(A)  x + y < -1

(B)  x + y > -1

(C)  x + y ≤ -1

(D)  x + y ≥ -1

Solution :

The slope-intercept form of the boundary line is

y = -x - 1

The standard form of the line is

x + y = -1

Since the boundary line is drawn as a dashed line, the inequality should not include an equal sign. Select a point in the plane which is not on the boundary line and test the inequalities in the answer choices. Let’s use (0, 0).

In option (A),

x + y > -1

0 + 0 > -1

0 > -1

0 > -1 (true)

In option (B),

x + y < -1

0 + 0 < -1

0 < -1

0 < -1 (false)

Therefore, the correct answer is option (A).

Problem 4 :

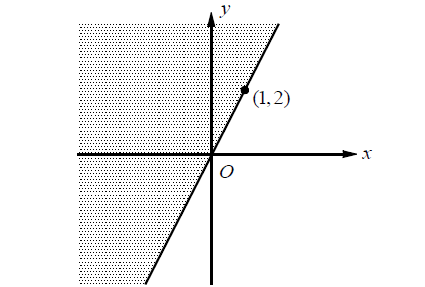
Which of the following inequalities represents the graph above?

(A)  2x - y ≥ 0

(B)  2x - y ≤ 0

(C)  x - 2y ≥ 0

(D)  x - 2y ≤ 0

Solution :

The slope-intercept form of the boundary line is

y = 2x

The standard form of the line is

2x - y = 0

Since the boundary line is drawn as a solid line, the inequality should include an equal sign. Select a point in the plane which is not on the boundary line and test the inequalities in the answer choices.

In this case, don't use (0, 0), because (0, 0) is on the boundary line.Let’s use (0, 1) .

In option (A),

2x - y  ≥ 0

2(0) - 1 ≥ 0

-1 ≥ 0

-1 ≥ 0 (false)

In option (B),

2x - y ≤ 0

2(0) - (1) ≤ 0

-1 ≤ 0

-1 ≤ 0 (true)

Therefore, the correct answer is option (B).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.