GRAPHING LINEAR INEQUALITIES IN TWO VARIABLES AND FIND COMMON REGION

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

In this section, we will learn, how to graph linear inequalities and find the solution using the common region in graph.

To obtain the common region for both the given linear inequalities, we have to follow the steps given below.

Step 1 :

First, we have to assume the given inequalities as equations.

Then, we have to draw the graph of the equations using any two or three points on the line.

Step 2 :

Take a point on either sides of the line, and substitute into the inequality and verify whether the inequality is satisfied by the point.

We have to shade the region from where the point is taken and it has satisfied the inequality.

Step 3 :

Do the process explained in step 2 for the second inequality.

Step 4 :

The region that is common to both the shaded portions is the solution to the system of inequalities.

Let us look at some examples based on the concept.

Example 1 :

Determine the region in the plane determined by the inequalities:

x ≤ 3y, x ≥ y

Solution :

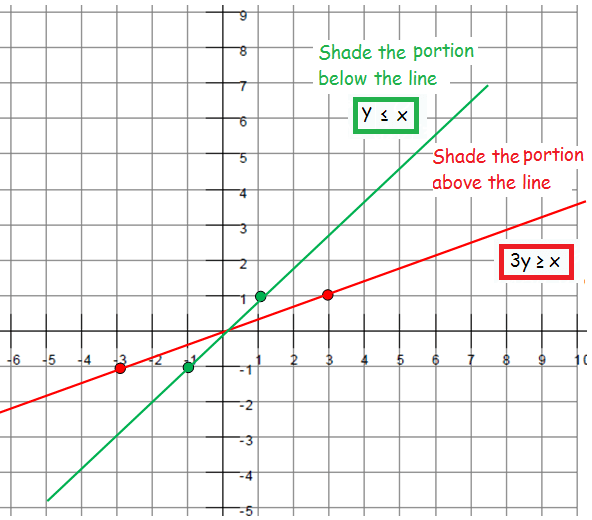
Given that : x ≤ 3y

3y ≥ x

3y = x

y = x/3

If x = -3, then y = -1

If x = 3, then y = 1

Given that : x ≥ y

y ≤ x

y = x

If x = -1, then y = -1

If x = 1, then y = 1

The points on the line y = x/3 are (-3, -1) and (3, 1)

The points on the line y = x are (-1, -1) and (1, 1)

Test point :

3y ≥ x

x = 0, and y = 0

Satisfies the inequality.

Since we have ≥, shade the portion above the line.

Test point :

y ≤ x

x = 0, and y = 0

Satisfies the inequality.

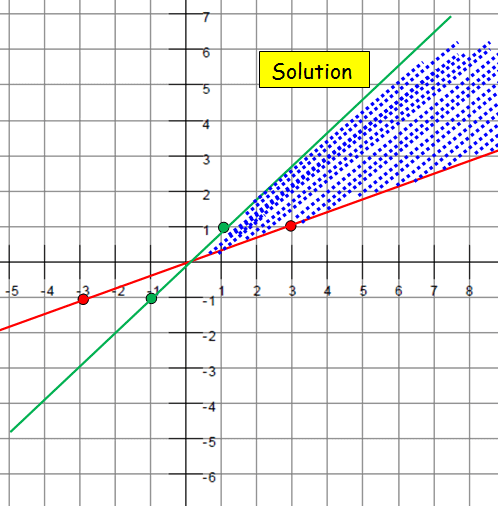
Example 2 :

Determine the region in the plane determined by the inequalities:

y ≥ 2x, −2x + 3y ≤ 6.

Solution :

Given that : y ≥ 2x

y = 2x

If x = -1, then y = -2

If x = 1, then y = 2

Given that : −2x + 3y ≤ 6

3y = 2x + 6

y = (2/3)x + (6/3)

y = (2x/3) + 2

If x = -3, then y = 0

If x = 3, then y = 4

The points on the line y ≥ 2x are (-1, -2) and (1, 2)

The points on the line −2x + 3y ≤ 6 are (-3, 0) and (3, 4)

Test point :

y ≥ 2x

x = 0, and y = 0

Satisfies the inequality.

Test point :

−2x + 3y ≤ 6

x = 0, and y = 0

Satisfies the inequality.

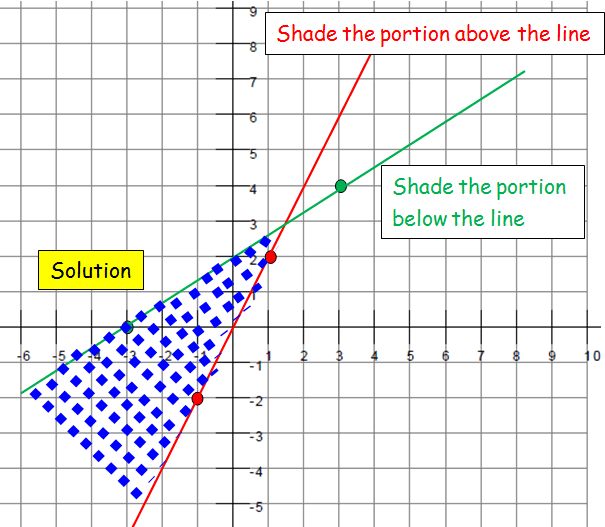
Example 3 :

Determine the region in the plane determined by the inequalities:

3x + 5y ≥ 45, x ≥ 0, y ≥ 0

Solution :

3x + 5y ≥ 45

5y ≥ 45 - 3x

y ≥ (45 - 3x)/5

y ≥ 9 - (3x/5)

Let y = 9 - (3x/5)

If x = 5

y = 9 - 3

y = 6

If x = 10

y = 9 - 6

y = 3

If x = 15

y = 9 - 9

y = 0

By joining the points (5, 6) (10, 3) and (15, 0).

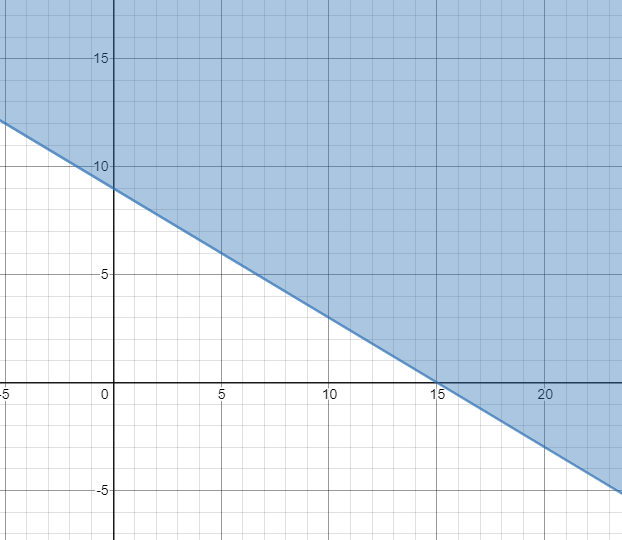
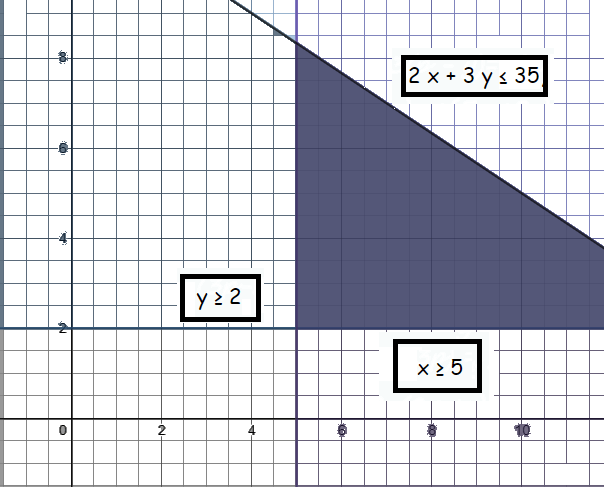
Example 4 :

Determine the region in the plane determined by the inequalities:

2 x + 3 y ≤ 35, y ≥ 2, x ≥ 5

Solution :

2 x + 3 y ≤ 35

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

About Us | Contact Us | Privacy Policy

GRAPHING LINEAR INEQUALITIES IN TWO VARIABLES AND FIND COMMON REGION

Recent Articles

Digital SAT Math Problems and Solutions (Part - 1)

AP Precalculus Problems and Solutions

SAT Math Preparation with Hard Questions