GRAPHING LINEAR FUNCTIONS WORKSHEET

1. Graph the linear function y = (2/3)x - 1.

2. Graph the linear function y = (-5/2)x + 3.

3. Ken has a weekly goal of burning 2400 calories by taking brisk walks. The equation y = -300x + 2400 represents the number of calories y Ken has left to burn after x hours of walking which burns 300 calories per hour. After how many hours of walking will Ken have 600 calories left to burn ? After how many hours will he reach his weekly goal?

4. The temperature at dawn was 8 °F and increased steadily 2 °F every hour. The equation y = 2x + 8 gives the temperature y after x hours. State whether the relationship between the time and the temperature is proportional or non proportional. Then graph the function.

5. The temperature of a fish tank was 82 °F and decreased steadily 2 °F every hour. The equation y = -2x + 82 gives the temperature y after x hours. State whether the relationship between the time and the temperature is proportional or non proportional. Then graph the function.

1. Answer :

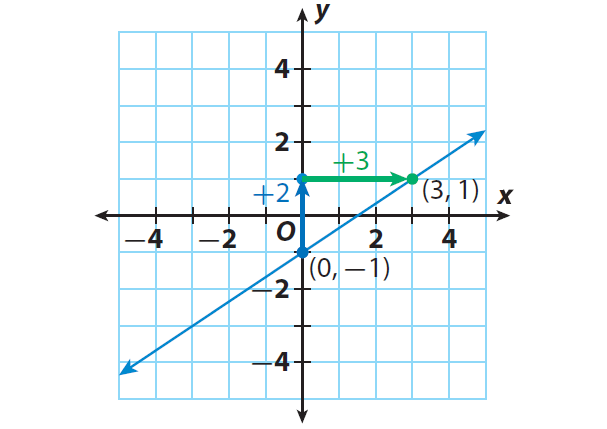
y = (2/3)x - 1

Step 1 :

The y-intercept is b = -1. Plot the point that contains the y-intercept : (0, -1).

Step 2 :

The slope is m = 2/3. Use the slope to find second a point. Since the slope = rise/run, from (0, -1), count up 2 units and right 3 units.

Then, the new point is (3, 1).

Step 3 :

Draw a line through the points.

2. Answer :

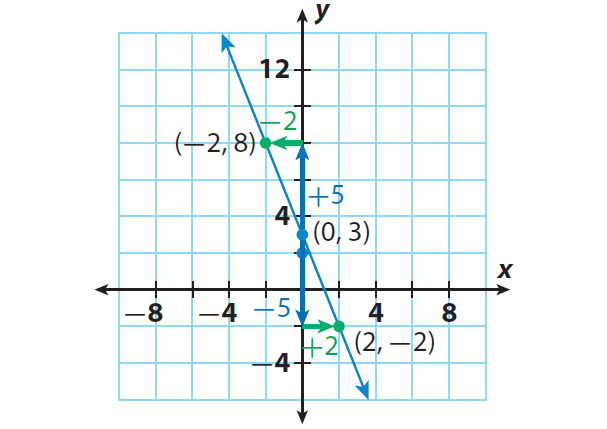
y = (-5/2)x + 3

Step 1 :

The y-intercept is b = 3. Plot the point that contains the y-intercept : (0, 3).

Step 2 :

The slope is m = -5/2. Use the slope to find second a point. Since the slope = rise/run, from (0, 3), count down 5 units and right 2 units or up 5 units and left 2 units.

Then, the new point is (2, -1) or (-2, 8).

Step 3 :

Draw a line through the points.

3. Answer :

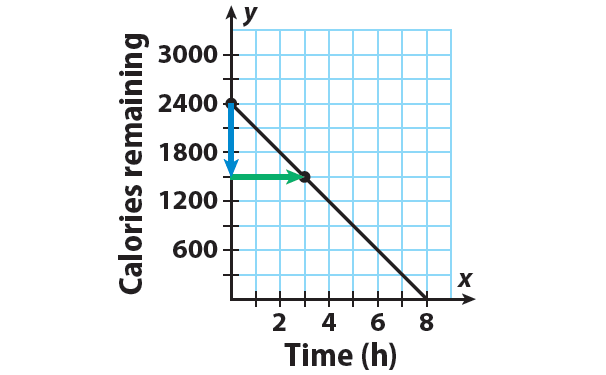
Step 1 :

 y = -300x + 2400

The y-intercept is b = 2400. Plot the point that contains the y-intercept : (0, 2400).

Step 2 :

Write the slope as a fraction.

m = -300/1 = -600/2 = -900/3

Using the slope as -900/3 helps in drawing a more accurate graph.

The slope is m = -900/3. Use the slope to find second a point. Since the slope  =  rise / run, from (0, 2400), count down 900 units and right 3 units.

Then, the new point is (3, 1500).

Step 3 :

Draw a line through the points.

Step 4 :

To find after how many hours of walking will Ken have 600 calories left to burn.

Locate 600 calories on the y-axis. Read across and down to the x-axis.

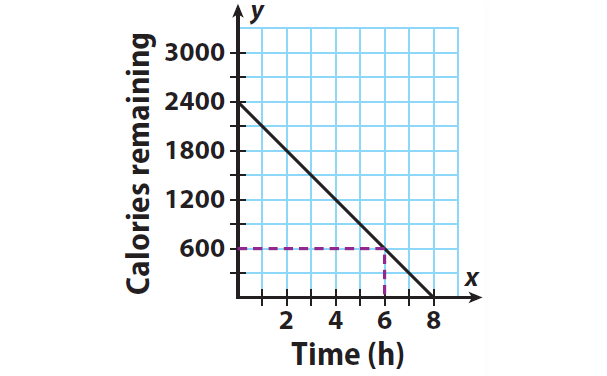
From the graph, we can know that Ken will have 600 calories left to burn after 6 hours.

Step 5 :

Ken will reach his weekly goal when the number of calories left to burn is 0. Because every point on the x-axis has a y-value of 0, find the point where the line crosses the x-axis.

Ken will reach his goal after 8 hours of brisk walking.

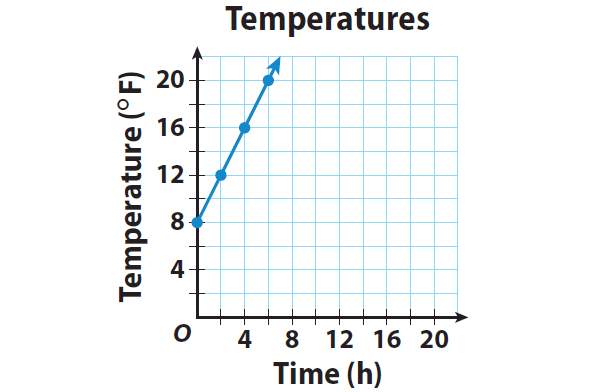
4. Answer :

Step 1 :

The given equation y = 2x + 8 is in slope-intercept form linear equation. That is, y = mx + b.

When we compare the equation y = 2x + 8 with y = mx + b, we get m = 2 and b = 8.

Therefore, the equation is a linear equation. Since b ≠ 0, the relationship is non proportional.

Step 2 :

Choose several values for the input x. Plug these values for x in the equation to find the output y.

Step 3 :

Graph the ordered pairs. Then draw a line through the points to represent the solutions of the function.

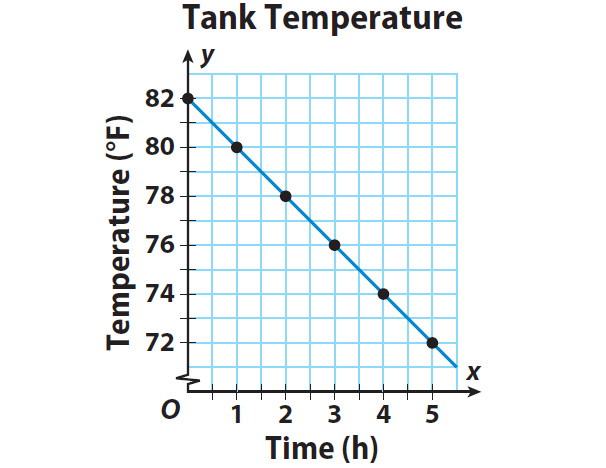
5. Answer :

Step 1 :

The given equation y = -2x + 82 is in slope-intercept form linear equation. That is, y = mx + b.

When we compare the equation y = -2x + 82 with y = mx + b, we get m = -2 and b = 82.

Therefore, the equation is a linear equation. Since b ≠ 0, the relationship is non proportional.

Step 2 :

Choose several values for the input x. Plug these values for x in the equation to find the output y.

Step 3 :

Graph the ordered pairs. Then draw a line through the points to represent the solutions of the function.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.