GRAPHING LINEAR EQUATIONS IN TWO VARIABLES WORKSHEET

Problem 1 :

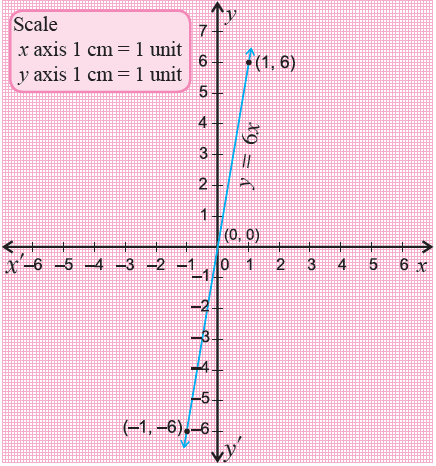
Graph y = 6x

Solution

Problem 2 :

Graph x = 5

Solution

Problem 3 :

Graph y = -5x/3 + 2

Solution

Problem 4 :

Graph 4x - y - 1 = 0

Solution

Problem 5 :

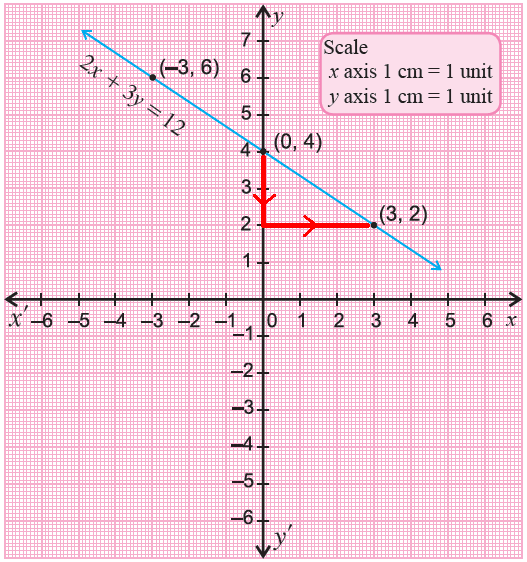
Graph 2x + 3y = 12

Solution

Problem 6 :

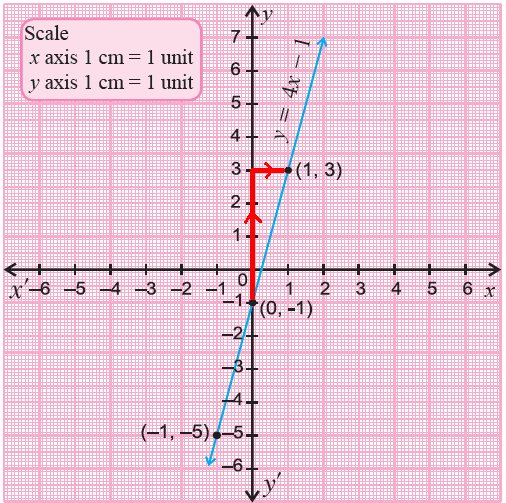
Graph y = 4x - 1 using its slope and y-intercept.

Solution

Problem 7 :

Graph y = -2x/3 + 4 using its slope and y-intercept.

Solution

Answer Key

1)  Plot the points (-1, -6), (0, 0) and (1, 6) on a xy-plane and connect them.

2)  Draw a straight line parallel to y-axis through the value '5' on the x-axis. 

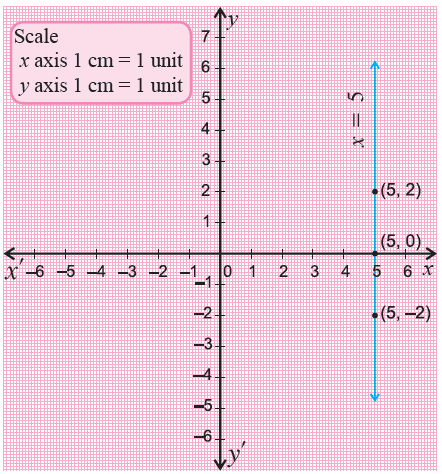
3)  Plot the points (-3, 7), (0, 2) and (3, -3) on a xy-plane and connect them.

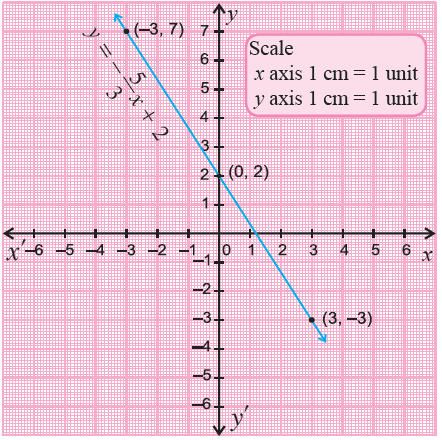
4)  Plot the points (-1, -5), (0, -1) and (1, 3) on a xy-plane and connect them.

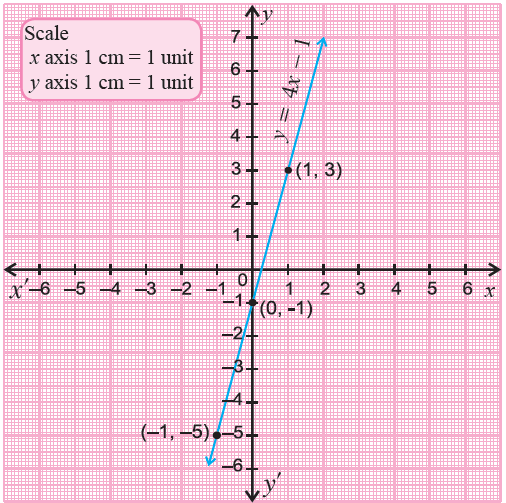
5)  Plot the points (-3, 6), (0, 4) and (3, 2) on a xy-plane and connect them.

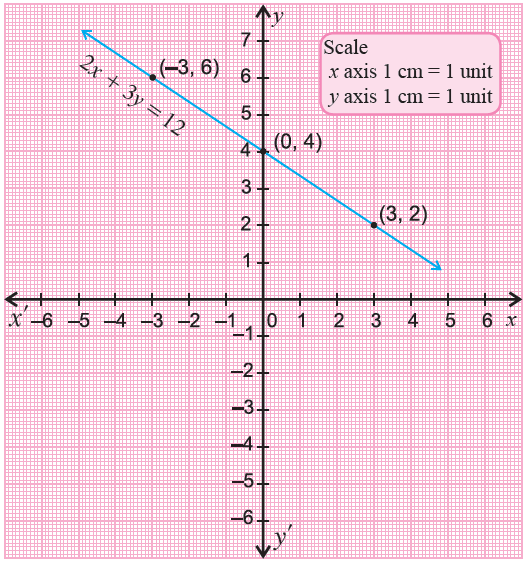
6)  Plot the two points (0, -1) and (1, 3) on a xy-plane connect them with a straight line.

7)  Plot the two points (0, 4) and (3, 2) on a xy-plane connect them with a straight line.

Since the rise = -2 is a negative value, we move 2 units down from (0, 4).

Problem 1 :

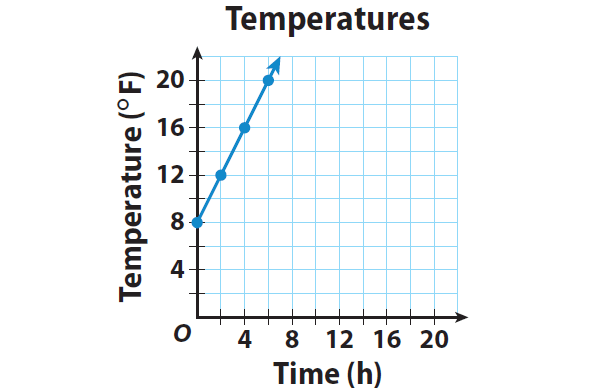
The temperature at dawn was 8 °F and increased steadily 2 °F every hour. The equation y = 2x + 8 gives the temperature y after x hours. State whether the relationship between the time and the temperature is proportional or non proportional. Then graph the function.

Solution

Problem 2 :

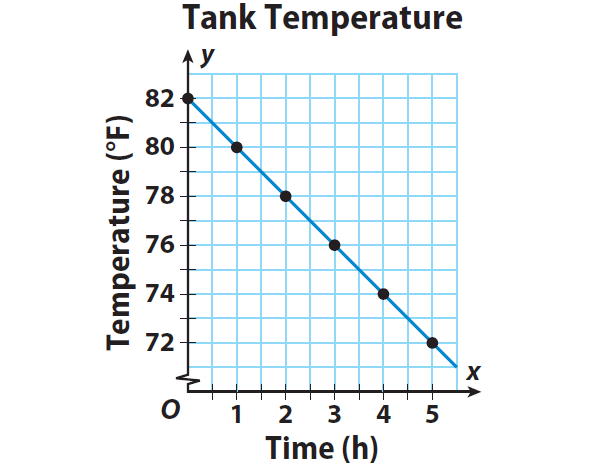
The temperature of a fish tank was 82 °F and decreased steadily 2 °F every hour. The equation y = -2x + 82 gives the temperature y after x hours. State whether the relationship between the time and the temperature is proportional or non proportional. Then graph the function.

Solution

Problem 3 :

Ellyn has a part-time job in a pizza restaurant. She receives $12 per hour for her work and is required to work between 1 and 4 hours in a shift.

a) Complete the following table of values:

b) Graph the points on a number grid.

c) Does it make sense to join the points? Why or why not?

d)  Use your graph to find:

i) how much Ellyn earns if she works 1.5 hours

ii) how long Ellyn must work to earn $30.

Solution

Problem 4 :

Daniel has $8 to spend on flowers for his garden bed. He buys x punnets of marigolds and y punnets of petunias. Each of the punnets costs $1, and he spends all of his money. 

a) Copy and complete this table which shows the different combinations he could buy

b) Graph the information in the table on a number grid.

c) Are the points collinear?

d) Write a relationship between x and y.

e) Is it meaningful to join the points with straight line segments?

Solution

Problem 5 :

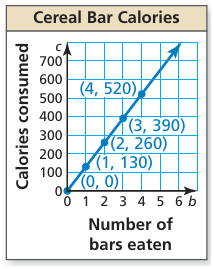
A cereal bar contains 130 calories. The number c of calories consumed is a function of the number b of bars eaten.

a. Does this situation represent a linear function? Explain.

b. Find the domain of the function. Is the domain discrete or continuous? Explain.

c. Graph the function using its domain.

d. Find the range of the function.

Solution

Answer Key

1)

2)

3)

a)

Hours worked (x) 1 2 3 4

Total pay (y) y = 12(1) ==> $12 y = 12(2) ==> $24 y = 12(3) ==> $36 y = 12(4) ==> $48

b)

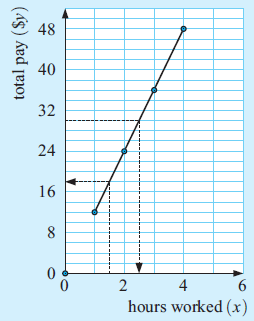
c) Yes, it makes sense to join the points because it is  possible for Ellyn to work part of an hour

d) i) Ellyn works 1.5 hours she earns $18.

ii)  To earn $30 Ellyn must work for 2.5 hours.

4)

a)

punnets of marigolds(x) 0 1 2 3 4 5 6 7 8

punnets of petunias(y) 8 7 6 5 4 3 2 1 0

b)

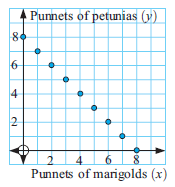
c) Yes, the points are collinear.

d) x + y = 8Write a relationship between x and y.

e) Yes, it creates a linear relationship. That's why we get the straight line as graphical form.

5)  a)  As b increases by 1, c increases by 130. The rate of change is constant.

b)   continuous.

c) the graph is a line with a domain of b ≥ 0.

d)  the range is c ≥ 0.

Copy and complete the following tables for the equations provided. Plot each set of ordered pairs on separate axes and draw straight lines through the points.

Problem 1 :

Solution

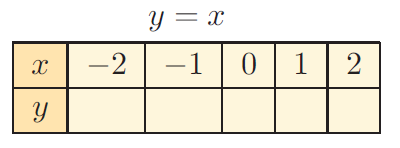
Problem 2 :

Solution

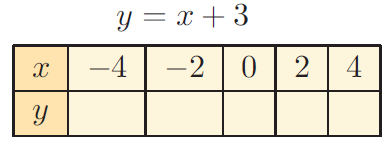
Problem 3 :

Solution

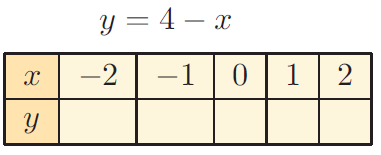
Problem 4 :

Solution

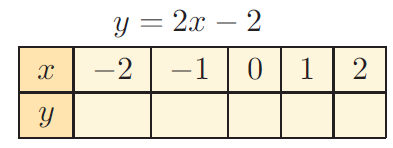
Problem 5 :

Solution

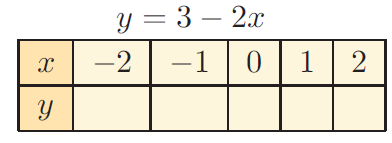
Problem 6 :

Solution

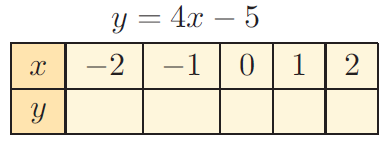
Problem 7 :

Solution

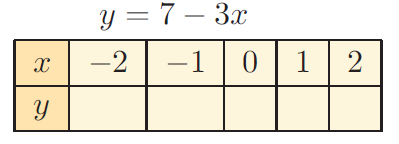
Problem 8 :

(a) Draw y = 3x − 4

(b) Draw x + y = 2

The graph y = 3x − 4 crosses the y-axis at the point A The graph x + y = 2 crosses the x-axis at the point B O is the origin.

(c) Write down the coordinates of the point A

(d) Write down the coordinates of the point B

(e) Find the area of triangle OAB

Solution

Answer Key

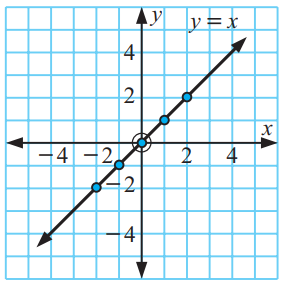
1)

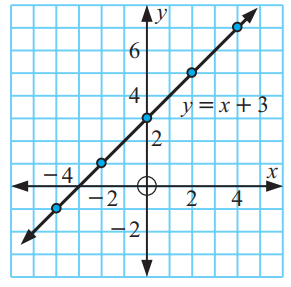
2)

3)

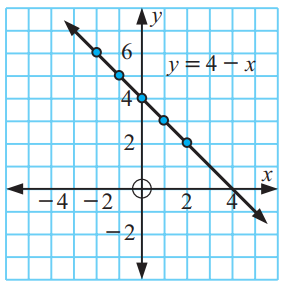
4)

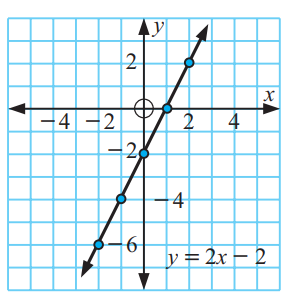
5)

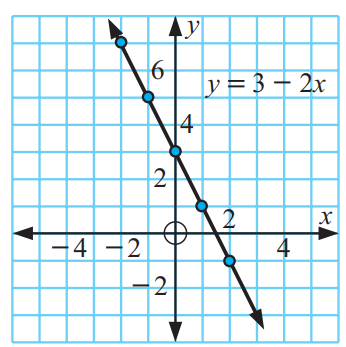
6)  

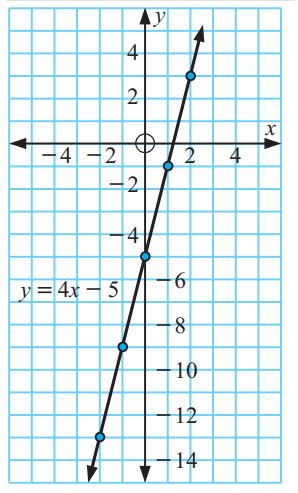
7)

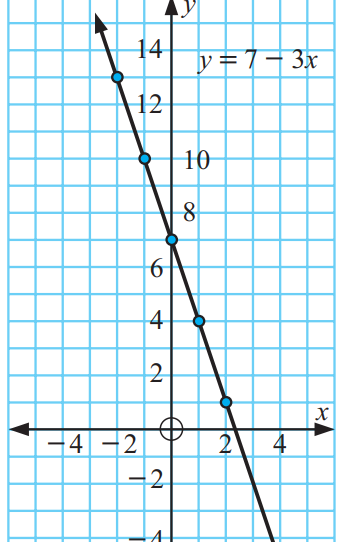
8) a) Drawing the line y = 3x + 4 using the coordinates.

(-2, -10)(-1, -7)(0, -4) (1, -1) (2, 2) and (3, 5)

b)  Drawing the line x + y = 2 using the coordinates. 

(-2, 4) (-1, 3) (0, 2) (1, 1) (2, 0) and (3, -1)

c)  A(0, -4)

d)  B(2, 0)

e) 

Area of triangle OAB = (1/2) x base x height

= (1/2) x 4 x 2

= 4 square units.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.