HOW TO SKETCH THE GRAPH OF SINUSOIDAL FUNCTION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The general form of a sinusoidal function :
y = a sin [k(x - b)] + N
To sketch the graph of a sinuoidal function, first we have to sketch the graph of a basic sine function, which is
y = sin (x)
We have one pattern of y = sin (x) from x = 0 to x = 2π.
Then, we have to apply the following transformations one by one in the given order to get the graph of the given sinusoidal function.
vertical strech/compression (a)
horizontal stretch/compression (k)
reflection over x-axis (if a < 0)
horizontal shift (b)
vertical shift (N)
Example :
Sketch the graph of
Solution :
Sketch the graph of y = sin (x).
When x = 0,
y = sin (0)
y = 0
y = 1
When x = π,
y = sin (π)
y = 0
y = -1
When x = 2π,
y = sin (2π)
y = 0
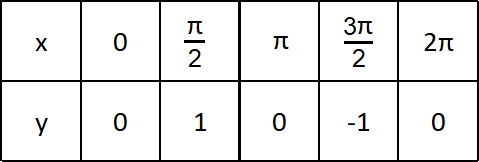
We get the following points from the above table.
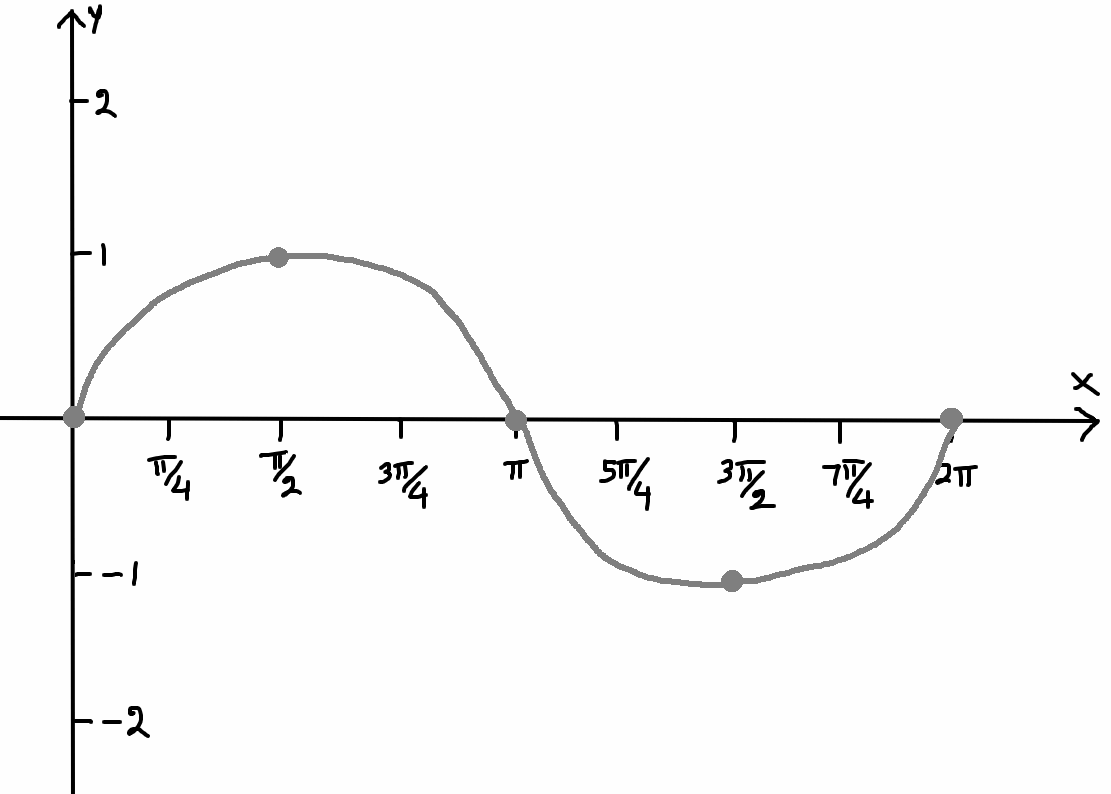
Plot the above points on a xy-plane and sketch the graph of y = sin (x).
Comparing
y = a sin [k(x - b)] + N
and
we get
a = 2 and k = 2
Vertical Stretch/Compression :
a = 2 refers to vertical stretch by a factor of 2.
That is, at each point on the above graph, multiply the y-coordinate by 2.
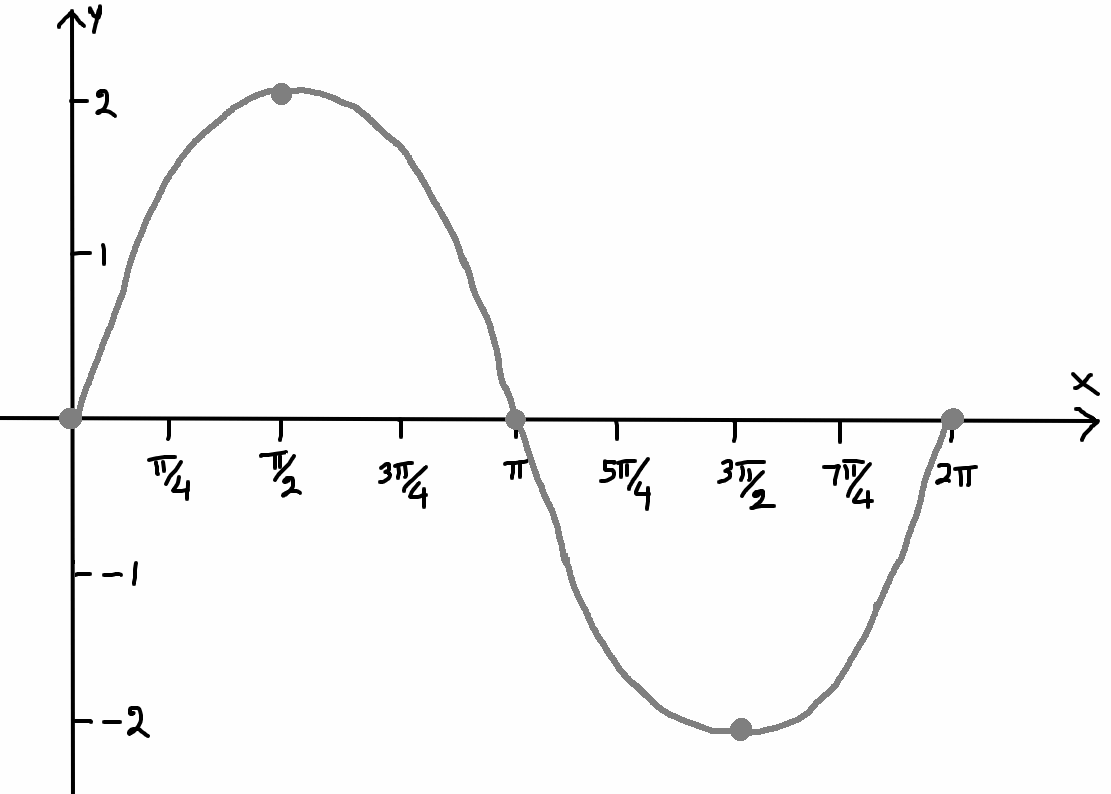
Horizontal Stretch/Compression :
k = 2 refers to horizontal compression by a factor of 2.
That is, at each point on the above graph, multiply the x-coordinate by ½.
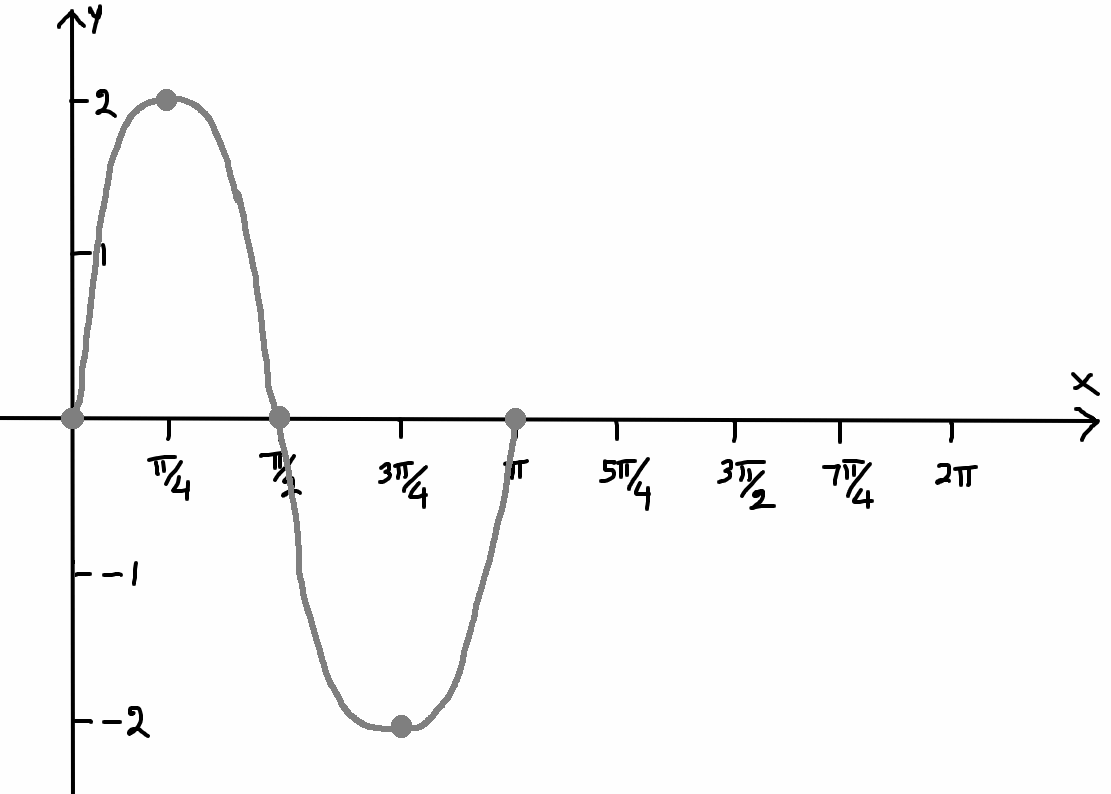
Horizontal Shift :
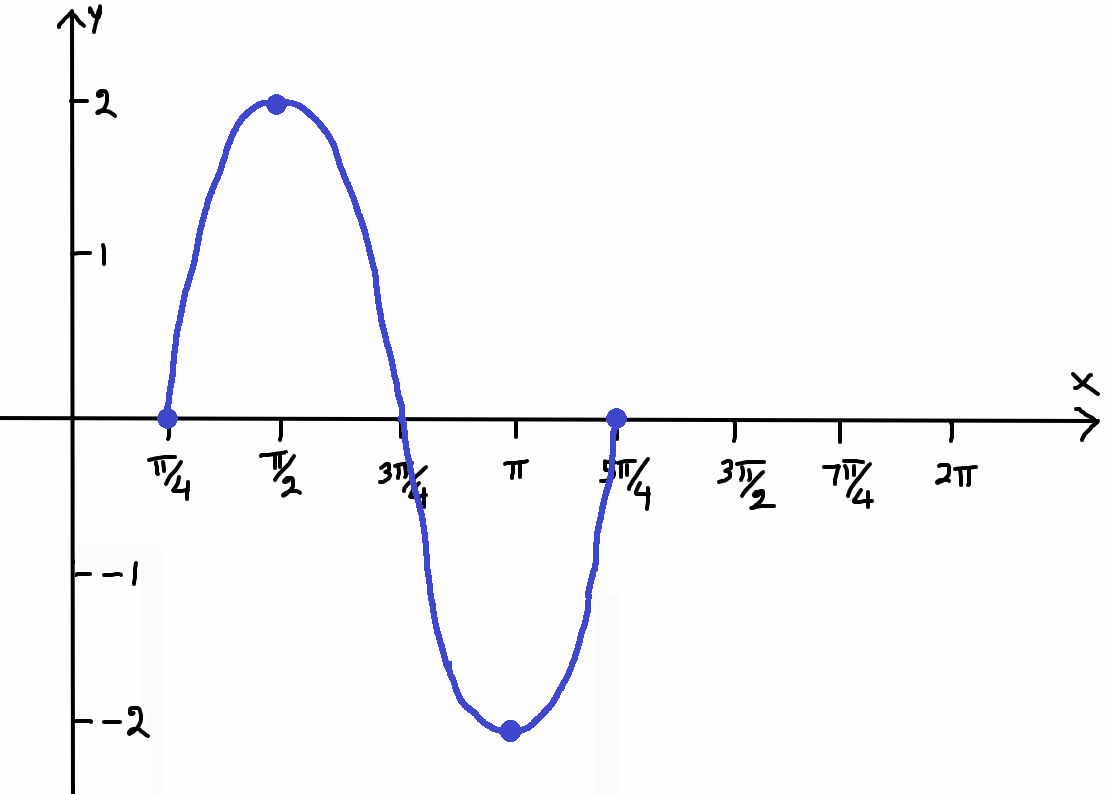
The above is the graph of the given sinusoidal function. In the given sinusoidal function, since there is no value at the place of N, there is no vertical shift.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

