GRAPHING LINEAR EQUATIONS IN TWO VARIABLES

The graph of a linear equation in two variables will be a straight line. 

Example 1 :

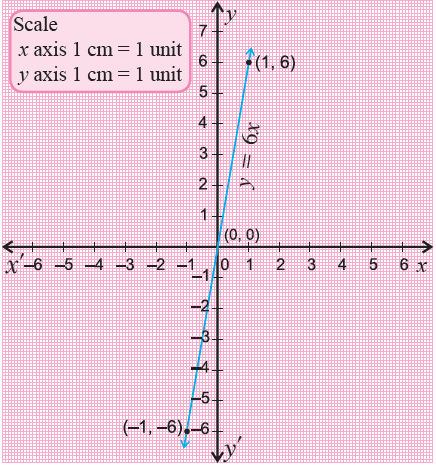
Graph y = 6x.

Solution :

The given equation is in slope-intercept form. Substitute some random values for x and find their corresponding values of y.

When x = -1,

y = 6(-1)

= -6

(-1, 6)

When x = 0,

y = 6(0)

= 0

(0, 0)

When x = 1,

y = 6(1)

= 6

(1, 6)

Plot the points (-1, -6), (0, 0) and (1, 6) on a xy-plane and connect them.

Example 2 :

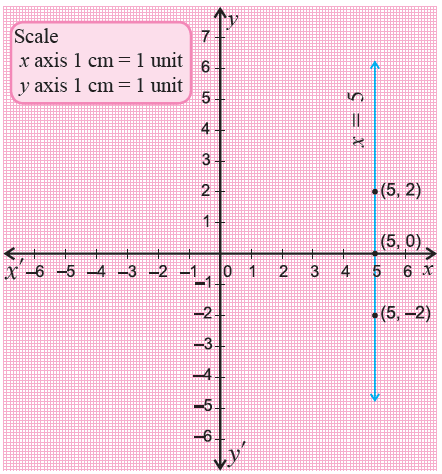
Graph x = 5.

Solution :

x = 5 is the equation of a line parallel to y-axis and also the line is passing through the value '5' on the x-axis.

Draw a straight line parallel to y-axis through the value '5' on the x-axis. 

Example 3 :

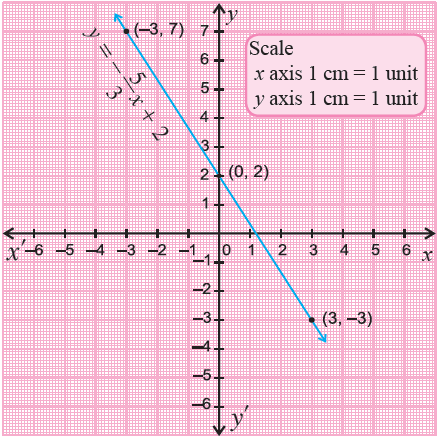
Graph y = -5x/3 + 2.

Solution :

The given equation is in slope-intercept form. Substitute some random values for x and find their corresponding values of y.

In the equation y = 5x/3 + 2, the denominator for the x-term is 3. So, substitute values for x which are the multiples of 3.

When you substitute values for x which are multiples of 3, the values of y will be integer and it will make our graphing process easier.

When x = -3,

y = -5(-3)/3 + 2

= 5 + 2

= 7

(-3, 7)

When x = 0,

y = -5(0)/3 + 2

= 0 + 2

(0, 2)

When x = 3,

y = -5(3)/3 + 2

= -5 + 2

= -3

(3, -3)

Plot the points (-3, 7), (0, 2) and (3, -3) on a xy-plane and connect them.

Example 4 :

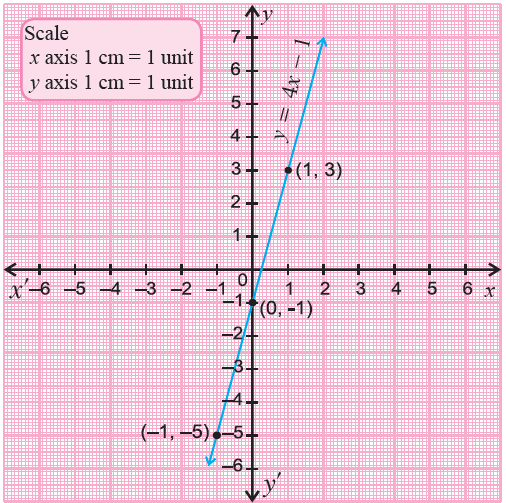
Graph 4x - y - 1 = 0.

Solution :

The given linear equation is not in slope-intercept form. Write the given equation is in slope intercept form.

4x - y - 1 = 0

Add y to both sides.

4x - 1 = y

or

y = 4x - 1

Now the equation is in slope-intercept form. Substitute some random values for x and find their corresponding values of y.

When x = -1,

y = 4(-1) - 1

= -4 - 1

(-1, -5)

When x = 0,

y = 4(0) - 1

= -1

(0, -1)

When x = 1,

y = 4(1) - 1

= 4 - 1

= 3

(1, 3)

Plot the points (-1, -5), (0, -1) and (1, 3) on a xy-plane and connect them.

Example 5 :

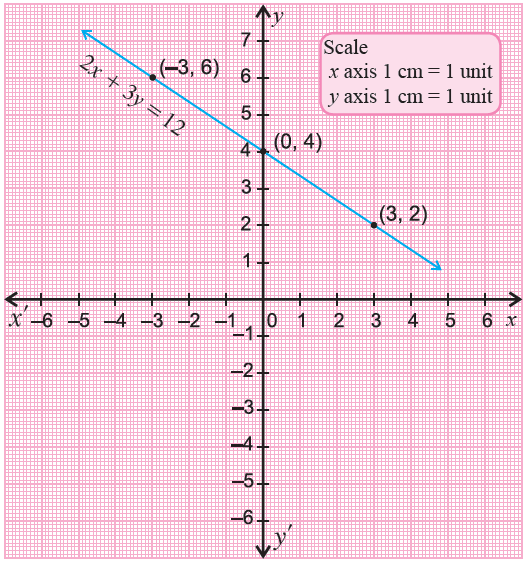
Graph 2x + 3y = 12.

Solution :

The given linear equation is not in slope-intercept form. Write the given equation is in slope intercept form.

2x + 3y = 12.

Subtract 2x from both sides.

3y = -2x + 12

Divide both sides by 3.

y = -2x/3 + 4

Now the equation is in slope-intercept form. Substitute some random values for x and find their corresponding values of y.

When x = -3,

y = -2(-3)/3 + 4

= 2 + 4

= 6

(-3, 6)

When x = 0,

y = -2(0)/3 + 4

= 0 + 4

= 4

(0, 4)

When x = 3,

y = -2(3)/3 + 4

= -2 + 4

= 2

(3, 2)

Plot the points (-3, 6), (0, 4) and (3, 2) on a xy-plane and connect them.

Graphing a Line Using the Slope and Y-Intercept

Example 6 :

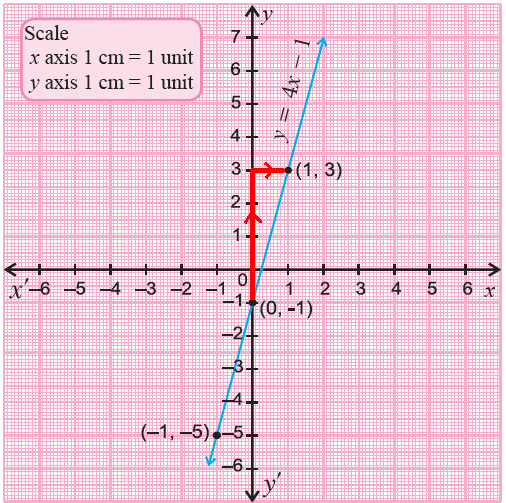
Graph y = 4x - 1.

Solution :

The given linear equation is in slope-intercept form.

Comparing y = mx + b and y = 4x - 1,

slope (m) = 4

y-intercept = -1 ----> (0, -1)

Using rise over run formula for slope,

rise/run = 4

rise/run = 4/1

rise = 4 and run = 1

Since the slope is positive, the graph will be a rising line.

We can do the following steps to graph the given linear equation.

Step 1 :

Plot the y-intercept (0, -1) on a xy-plane.

Step 2 :

rise = 4 ----> move 4 units up from (0, -1)

run = 1 ----> move 1 unit to the right further to (1, 3)

Plot the two points (0, -1) and (1, 3) on a xy-plane connect them with a straight line.

Note :

Since the rise = 4 is a positive value, we move 4 units up from (0, -1).

Incase the rise is a negative value, we have to move down. And for the run, always we have to move to the right.

Example 7 :

Graph y = -2x/3 + 4.

Solution :

The given linear equation is in slope-intercept form.

Comparing y = mx + b and y = -2x/3 + 4,

slope (m) = -2/3

y-intercept = 4 ----> (0, 4)

Using rise over run formula for slope,

rise/run = -2/3

rise = -2 and run = 3

Since the slope is positive, the graph will be a falling line.

We can do the following steps to graph the given linear equation.

Step 1 :

Plot the y-intercept (0, 4) on a xy-plane.

Step 2 :

rise = -2 ----> move 2 units down from (0, 4)

run = 3 ----> move 3 units to the right further to (3, 2)

Plot the two points (0, 4) and (3, 2) on a xy-plane connect them with a straight line.

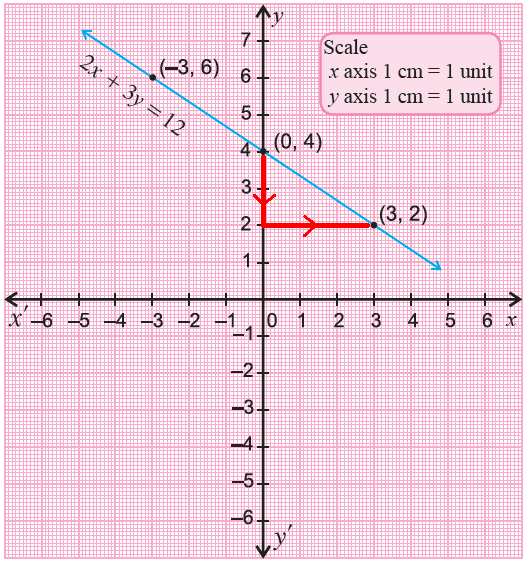
Since the rise = -2 is a negative value, we move 2 units down from (0, 4).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.