GRAPH INTEGERS ON HORIZONTAL AND VERTICAL NUMBER LINES

Horizontal Number Line :

Draw a line horizontally and mark some points at equal distance on it as shown in the figure.

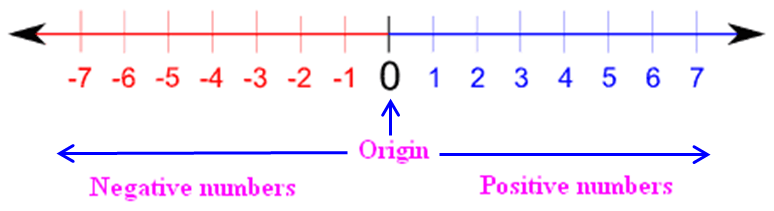
Mark a point as zero on it. Points to the right of zero are positive integers and are marked +1, +2, +3, etc. or simply 1, 2, 3 etc.

Points to the left of zero are negative integers and are marked –1, –2, –3 etc. In order to mark –6 on this line, we move 6 points to the left of zero.

Vertical Number Line :

Draw a line vertically and mark some points at equal distance on it as shown in the figure.

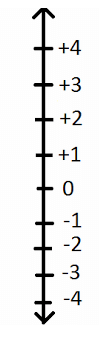
Mark a point as zero on it. Points to the upward of zero are positive integers and are marked +1, +2, +3, etc. or simply 1, 2, 3 etc.

Points to the upward of zero are negative integers and are marked –1, –2, –3 etc. In order to mark – 6 on this line, we move 6 points to the left of zero.

Example 1 :

The below vertical number line, representing integers. Observe it and locate the following points :

(a) If point D is + 8, then which point is – 8?

(b) Is point G a negative integer or a positive integer?

Solution :

(a) To find the position of the number -8, first let us mark down the points vertically on the given number line.

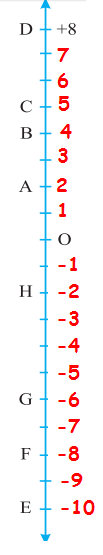
By marking the point on the given number line, we come to know that -8 is at the position F.

(b) By observing the number line "G" is below 0. Hence it is negative.

Example 2 :

Following is the list of temperatures of five places in India on a particular day of the year.

Plot the name of the city against its temperature and find the coolest place.

Solution :

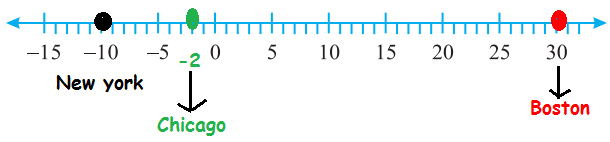
From the above horizontal number line, it is clear that New York is the coolest place.

Example 3 :

On which number line does point P best represent a distance of 1.09 units from 0?

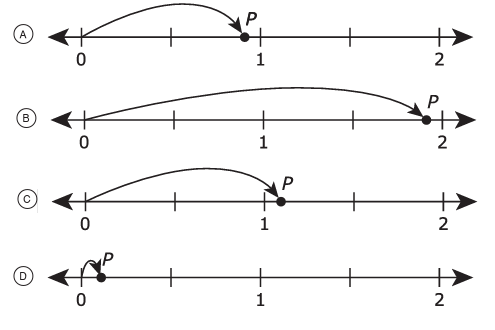
Solution :

Option c is correct.

Example 4 :

You deliver flowers to an office building. You enter at ground level and go down 2 floors to make the first delivery. Then you go up 7 floors to make the second delivery.

a) Write an integer that represents each position.

b)  Write an integer that represents how you return to ground level.

Solution :

a)

b)

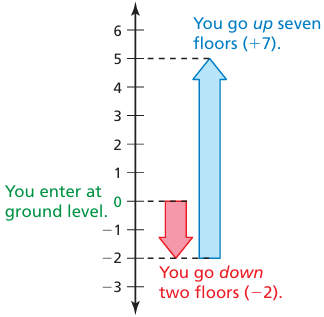
Use a number line to model your movement, as shown. The second delivery is on the fifth floor. You must go down 5 floors to return to ground level. The integer representing “down 5 floors” is − 5.

Example 5 :

Identify the integer represented by the point on the number line.

A, B , C and D

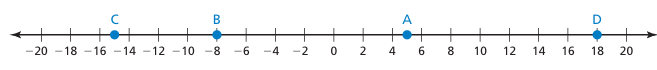
Solution :

• A represents +5
• B represents -8
• C represents -15
• D represents 18.

Example 6 :

Use the information below.

• Low tide is 1 foot below the average water level.
• High tide is 5 feet higher than low tide.

Write an integer that represents the average water level relative to high tide.

Solution :

Position f average water level is 0.

• Position of low tide is 1 foot below the average water level. The the required integer is -1.
• Position of high tide is 5 feet higher than position of low tide. Then the required position is 4. 

Example 7 :

Choose any positive integer.

a. Find the opposite of the integer.

b. Find the opposite of the integer in part (a).

c. What can you conclude about the opposite of the opposite of the integer?

Is this true for all integers? Use a number line to justify your answer.

d. Describe the meaning of −(−(−6)). Find its value.

Solution :

a) 

• Let 5 be the number, its opposite will be -5
• Let -3 be a number, its opposite will be 3.

b)

• Opposite of -5 is 5.
• Opposite of 3 is -3.

c) Opposite of opposite of the integer is the original number.

d)   −(−(−6))

Opposite of -6 is -(-6), then it is 6

Opposite of 6 is -6

Then the result is -6.

Example 8 :

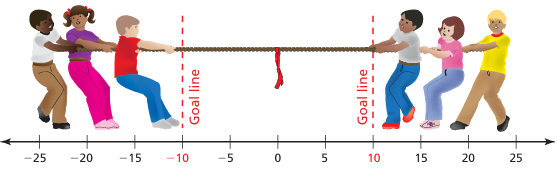
In a game of tug-of-war, a team wins by pulling the flag over its goal line. The flag begins at 0. During a game, the flag moves 8 feet to the right, 12 feet to the left, and 13 feet back to the right. Did a team win? Explain.

Solution :

• Start at position 0 feet.
• Move 8 feet to the right: 0 + 8 = 8 feet.
• Move 12 feet to the left: 8 - 12 = -4 feet.
• Move 13 feet to the right: -4 + 13 = 9 feet.

Since the final position is 9 feet to the right of the starting point (0 feet), a team did win.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.