GRAPH AND SOLVE QUADRATIC INEQUALITIES WORKSHEET
Graph and Solve Quadratic Inequalities Worksheet :
Worksheet given in this section will be much useful for the students who would like to practice problems on graphing and solving quadratic inequalities.
Graph and Solve Quadratic Inequalities Worksheet - Problems
Problem 1 :
Graph and solve for x :
x² - 7x + 6 > 0
Problem 2 :
Graph and solve for x :
-x² + 3x - 2 > 0
Problem 3 :
Graph and solve for x :
4x² - 25 ≥ 0
Problem 4 :
Graph and solve for x :
2x² − 12x + 50 ≤ 0
Graph and Solve Quadratic Inequalities Worksheet - Solutions
Problem 1 :
Graph and solve for x :
x² - 7x + 6 > 0
Solution :
x² - 7x + 6 > 0
(x - 1)(x - 6) > 0
On equating the factors to zero, we see that x = 1, x = 6 are the roots of the quadratic equation. Plotting these roots on real line and marking positive and negative alternatively from the right most part we obtain the corresponding number line as
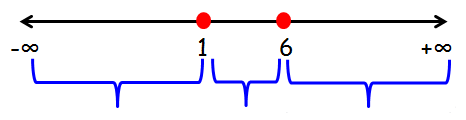
If we plot these points on the number line, we will get intervals (-∞, 1) (1, 6) (6, ∞).
|
From (-∞, 1) let us take -1 |
(-1 − 1) (-1 − 6) > 0 -2(-7) > 0 14 > 0 True |
|
From (1, 6) let us take 4 |
(4 − 1) (4 − 6) > 0 3(-2) > 0 -6 > 0 False |
|
From (6, ∞) let us take 7 |
(7 − 1) (7 − 6) > 0 6(1) > 0 6 > 0 True |
Hence, the solution set is
(− ∞, 1) ∪ (6, ∞)
Problem 2 :
Graph and solve for x :
-x² + 3x - 2 > 0
Solution :
-x² + 3x - 2 > 0
Multiplying by negative sign on both sides
x²- 3x + 2 < 0
(x − 1) (x − 2) < 0
x - 1 = 0 x - 2 = 0
x = 1 and x = 2
On equating the factors to zero, we see that x = 1, x = 2 are the roots of the quadratic equation. Plotting these roots on real line and marking positive and negative alternatively from the right most part we obtain the corresponding number line as
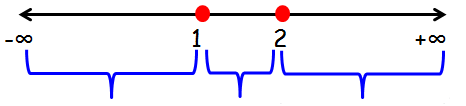
If we plot these points on the number line, we will get intervals (-∞, 1) (1, 2) (2, ∞).
|
From (-∞, 1) let us take -1 |
(x − 1) (x − 2) < 0 (-1 − 1) (-1 − 2) < 0 (-2)(-3) > 0 6 < 0 False |
|
From (1, 2) let us take 1.5 |
(x − 1) (x − 2) < 0 (1.5 − 1) (1.5 − 2) < 0 (-0.5)(-0.5) > 0 0.25 < 0 True |
|
From (2, ∞) let us take 7 |
(7 − 1) (7 − 6) > 0 6(1) > 0 6 > 0 False |
Hence, the solution set is
(1, 2)
Problem 3 :
Graph and solve for x :
4x² - 25 ≥ 0
Solution :
4x² - 25 ≥ 0
(2x)² - 5² ≥ 0
(2x - 5) (2x + 5) ≥ 0
2x - 5 ≥ 0 (or) 2x + 5 ≥ 0
x = 5/2 (or) x = -5/2
On equating the factors to zero, we see that x = 5/2, x = -5/2 are the roots of the quadratic equation. Plotting these roots on real line and marking positive and negative alternatively from the right most part we obtain the corresponding number line as
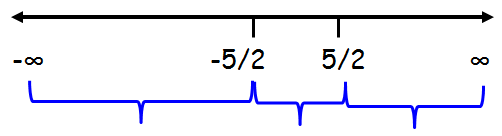
If we plot these points on the number line, we will get intervals (-∞, -5/2) (-5/2, 5/2) (5/2, ∞).Graph solutions to quadratic inequalities
|
From (-∞, -5/2) let us take -3 |
(2x - 5) (2x + 5) ≥ 0 (-6 − 5) (-6 + 5) < 0 (-11)(-1) > 0 11 > 0 True |
|
From (-5/2, 5/2) let us take 0 |
(2x - 5) (2x + 5) ≥ 0 (0− 5) (0 + 5) < 0 (-5)(5) > 0 -25 > 0 False |
|
From (5/2, ∞) let us take 4 |
(2x - 5) (2x + 5) ≥ 0 (8 − 5) (8 + 5) < 0 (3)(13) > 0 39 > 0 True |
Hence, the solution set is
(-∞, -5/2) U (5/2, ∞)
Problem 4 :
Graph and solve for x :
2x² − 12x + 50 ≤ 0
Solution :
2x² − 12x + 50 ≤ 0
2(x²− 6x + 25) ≤ 0
x² − 6x + 25 ≤ 0
(x²− 6x + 9) + 25 − 9 ≤ 0
(x − 3)² + 16 ≤ 0
This is not true for any real value of x.
So, the given quadratic inequality has no solution.
After having gone through the stuff given above, we hope that the students would have understood, how to graph and solve quadratic inequalities.
Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Writing Quadratic Functions in Standard Form
Apr 26, 24 12:39 PM
Writing Quadratic Functions in Standard Form or Vertex Form -
Factoring Quadratic Trinomials
Apr 26, 24 01:51 AM
Factoring Quadratic Trinomials - Key Concepts - Solved Problems -
Factoring Trinomials Worksheet
Apr 25, 24 08:40 PM
Factoring Trinomials Worksheet