GRAPH A LINEAR INEQUALITY IN THE COORDINATE PLANE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
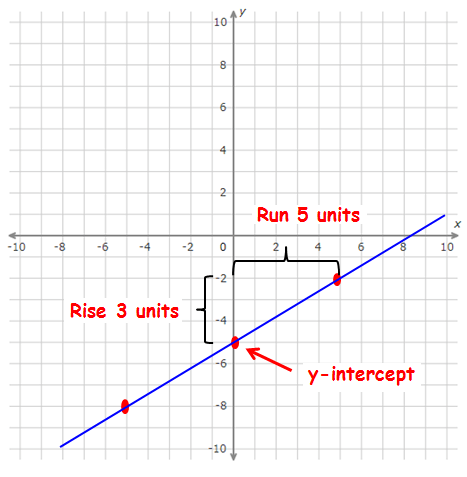
The following steps will be useful to graph a linear inequality in the coordinate plane.
Step 1 :
Consider the given inequality as equation and write the equation in slope-intercept form.
That is,
y = mx + b
Draw the boundary line using slope and y-intercept of the line.
Step 2 :
We have to use a solid line, if the given equation is having the signs ≥ or ≤.
We have to use a dotted line, if the given equation is having the signs < or >.
Step 3 :
After drawing the boundary line, we have to take a point on either sides of the line and check which point satisfies the given inequality.
We have to shade the region from where the point that satisfies the given inequality is taken.
Example 1 :
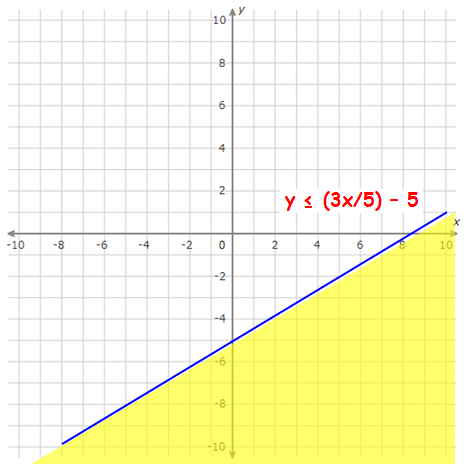
Sketch the graph of the following linear inequality.
y ≤ (3x/5) - 5
Solution :
Step 1 :
Consider the given inequality as equation.
y = (3x/5) - 5
The equation above is in slope-intercept form.
Slope = 3/5
y-intercept = -5
Using the slope and y-intercept, sketch the graph of the line.
Step 2 :
Take a point on either sides of the line and check which point satisfies the given inequality.
|
Test point 1 : (5, -5) x = 5 and y = -5 y ≤ (3x/5) - 5 -5 ≤ (3(5)/5) - 5 -5 ≤ (15/5) - 5 -5 ≤ 3 - 5 -5 ≤ - 2 true |
Test point 2 : (-5, -4) x = -5 and y = -4 y ≤ (3x/5) - 5 -4 ≤ (3(-5)/5) - 5 -4 ≤ (-15/5) - 5 -4 ≤ -3 - 5 -4 ≤ -8 false |
Step 3 :
From the above step, the point (5, -5) satisfies the inequality.
So, we have to shade the region from where the point (5, -5) is taken.
Example 2 :
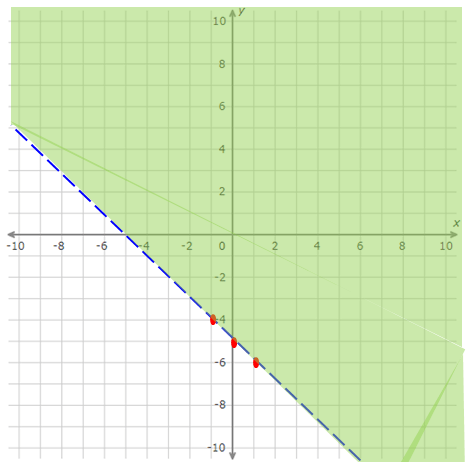
Sketch the graph of the following linear inequality.
y > -x - 5
Solution :
As we have done in example 1, we can do steps 1, 2 and 3 and get the graph of the inequality as shown below.
Example 3 :
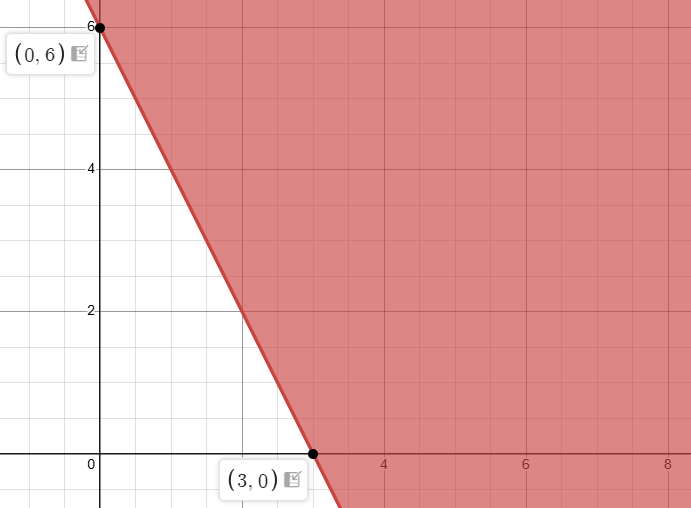
An online store sells digital cameras and cell phones. The store makes a $100 profit on the sale of each digital camera x and a $50 profit on the sale of each cell phone y. The store wants to make a profit of at least $300 from its sales of digital cameras and cell phones. Write and graph an inequality that represents how many digital cameras and cell phones they must sell. Identify and interpret two solutions of the inequality.
Solution :
100x + 50y ≥ 300
50y ≥ -100 x + 300
y ≥ (-100/50) x + (300/50)
y ≥ -2x + 6
|
When x = 1 y = -2(1) + 6 y = -2 + 6 y = 4 |
When x = 2 y = -2(2) + 6 y = -4 + 6 y = 2 |
|
When x = 3 y = -2(3) + 6 y = -6 + 6 y = 0 |
y-intercept : Put x = 0 -2(0) + 6 = y 6 = y |
(1, 4) (2, 2) (3, 0) and (0, 6)
Example 4 :
Which ordered pair is not a solution of
x + 5y < 15
a) (-1, -3) b) (-1, 3) c) (1, 3) d) (3, 2)
Solution :
x + 5y < 15
Option a :
Applying the point (-1, -3) in the inequality given, we get
-1 + 5(-3) < 15
-1 - 15 < 15
-16 < 15
is a solution.
Option b :
Applying the point (-1, 3) in the inequality given, we get
-1 + 5(3) < 15
-1 + 15 < 15
14 < 15
is a solution.
Option c :
Applying the point (1, 3) in the inequality given, we get
1 + 5(3) < 15
1 + 15 < 15
16 < 15
is not a solution.
Option d :
Applying the point (3, 2) in the inequality given, we get
3 + 5(2) < 15
3 + 10 < 15
13 < 15
is a solution.
Option c is correct.
Example 5 :
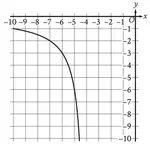
The graph of which inequality is shown ?
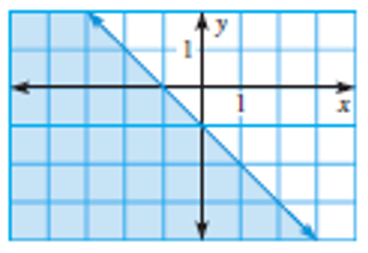
a) x + y ≤ -1 b) x + y ≥ -1 c) x - y ≤ -1 b) x - y ≥ -1
Solution :
The shaded region is below the line,
slope = rise / run
= -1/1
m = -1
y-intercept = -1
y = mx + b
y = -1x - 1
Choosing one of the points from the shaded region (-1, -1)
-1 = -1(-1) - 1
-1 = 1 - 1
-1 = 0
Since it is solid line, it must be a less than or equal or greater than or equal sign.
x + y ≤ -1
Example 6 :
The inequality 9x + 5y ≥ 60 represents the number x of newspapers and the number y of magazines you must sell to earn enough points to earn a special school lunch. You sell four newspapers and six magazines. Do you receive a special school lunch? Explain.
Solution :
9x + 5y ≥ 60
x is the number of newspapers and y is the number of magazines.
x = 4 and y = 6
9(4) + 5(6) ≥ 60
36 + 54 ≥ 60
90 ≥ 60
Since the given point satisfies the inequality given, it must be the solution. Then you receive special school lunch.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Questions and Answers (Part - 3)
Mar 13, 26 08:41 PM
Digital SAT Math Questions and Answers (Part - 3) -
Digital SAT Math Problems and Solutions (Part - 50)
Mar 13, 26 10:25 AM
Digital SAT Math Problems and Solutions (Part - 50) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Mar 13, 26 02:08 AM
SAT Math Resources (Videos, Concepts, Worksheets and More)