GRAPH A LINEAR INEQUALITY IN ONE VARIABLE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To graph a linear inequality in one variable, first we have to draw a number line.
Now we have to draw a arrow to represent the given inequality.
For example x < 5 means the value of the variable x is lesser than 5. So it may be 4, 3, 2, 1, 0. We have to graph the given linear inequality as follows.

When we have the symbol < or > inequality in the given question, we have to use open circle.
When we have the symbol ≤ or ≥ inequality in the given question, we have to use closed circle.
Example 1 :
Graph the solutions of the inequality x ≥ -2. Check the solutions.
Solution :
Step 1 :
Draw a closed circle at -2 to show that -3 is a solution.
Step 2 :
Shade the number line to the right of -2 to show that numbers greater than -2 are solutions.

(Use a solid circle for an inequality that uses ≥ or ≤)
Step 3 :
Check your solution.
Choose a number that is on the shaded section of the number line, such as -1.
Substitute -1 for x.
-1 ≥ -2
-1 is greater than -2, so -1 is a solution.
Step 4 :
Let us prove that -2 is a solution of the inequality x ≥ -2.
In the given inequality, plug y = -2.
Then, we have
-2 ≤ -2 ---> (-2 is greater than or equal to -2) ?
Is the answer for the above question is "yes or "no" ?
The answer for the above question is "Yes".
Because, -2 is equal to -2.
Hence, -2 is a solution to the inequality x ≥ -2.
Example 2 :
Graph the solutions of the inequality x ≥ 6. Check the solutions.
Solution :
Step 1 :
Draw a closed circle at 6 to show that 6 is a solution.
Step 2 :
Shade the number line to the right of 6 to show that numbers greater than 6 are solutions.

(Use a solid circle for an inequality that uses ≥ or ≤)
Step 3 :
Check your solution.
Choose a number that is on the shaded section of the number line, such as 7.
Substitute 7 for x.
7 ≥ 6
7 is greater than 6, so 6 is a solution.
Step 4 :
Let us prove that 6 is a solution of the inequality x ≥ 6.
In the given inequality, plug y = 6.
Then, we have
6 ≤ 6 ---> (6 is greater than or equal to 6) ?
Is the answer for the above question is "yes or "no" ?
The answer for the above question is "Yes".
Because, 6 is equal to 6.
Hence, 6 is a solution to the inequality x ≥ 6.
Example 3 :
Graph the solutions of the inequality 1 < m. Check the solutions.
Solution :
Step 1 :
Draw an empty circle at 1 to show that 1 is not a solution.
Step 2 :
Shade the number line to the right of 1 to show that numbers greater than 1 are solutions.

(Use an open circle for an inequality that uses > or <)
Step 3 :
Check your solution.
Choose a number that is on the shaded section of the number line, such as 2.
Substitute -4 for y.
1 < 2
1 is less than 2, so 2 is a solution.
Step 4 :
Let us prove that 1 is not a solution of the inequality 1 < m.
In the given inequality, plug m = 1.
Then, we have
1 < 1 ---> (1 is less than 1) ?
Is the answer for the above question is "yes or "no" ?
The answer for the above question is "No".
Because, 1 is equal to 1.
Hence, 1 is not a solution to the inequality 1 < m.
Example 4 :
Graph the solutions of the inequality t ≤ -4. Check the solutions.
Solution :
Step 1 :
Draw a solid circle at -4 to show that -4 is a solution.
Step 2 :
Shade the number line to the left of -4 to show that numbers less than -4 are solutions.
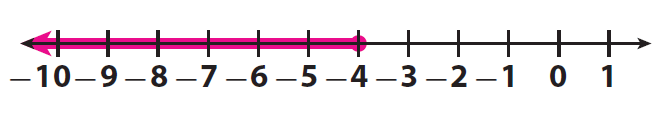
(Use a solid circle for an inequality that uses ≥ or ≤)
Step 3 :
Check your solution.
Choose a number that is on the shaded section of the number line, such as -5.
Substitute -5 for t.
-5 ≤ -4
-5 is less than -4, so -5 is a solution.
Step 4 :
Let us prove that -4 is a solution of the inequality t ≤ -4.
In the given inequality, plug t = -4.
Then, we have
-4 ≤ -4 ---> (-4 is less than or equal to -4) ?
Is the answer for the above question is "yes or "no" ?
The answer for the above question is "Yes".
Because, -4 is equal to -4.
Hence, -4 is a solution to the inequality t ≤ -4.
Example 5 :
Each day at lunchtime, at least 53 people buy food from a food truck. Write an inequality that represents this situation.
Solution :
Let x be the number of people.
x ≥ 53
Example 6 :
A subway ride for a student costs $1.25. A monthly pass costs $35.
a. Write an inequality that represents the number of times you must ride the subway for the monthly pass to be a better deal.
b. You ride the subway about 45 times per month. Should you buy the monthly pass? Explain.
Solution :
a) Cost for a ride = $1.25
Monthly pass = $35
Let x be the number of times you must ride the subway.
35 > 1.25x
35 / 1.25 > x
28 > x
The maximum number of times is 28.
b) Number of times the subway = 45
= 35/45
= 0.7
To have one ride since we need to spend 1.25, since the above cost is lesser than 1.25, we may buy the monthly pass.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

