GRADE 10 MATH PRACTICE TEST WITH SOLUTION

Problem 1 :

Find the 12^th term of an arithmetic progression

6, 1, -4, ...........

Solution :

a  =  6, d  =  1 - 6 ==>  -5

a_n  =  a + (n-1)d

a₁₂  =  6 + (12-1)(-5)

a₁₂  =  6 + 11(-5)

a₁₂  =  6 - 55

a₁₂  =  - 49

Problem 2 :

If a clock strikes appropriate number of times at each hour how many times will it strike in a day ? 

Solution :

Clock will strike 1 time at 1'o clock, 2 times at 2'o clock and so on.

1+2+3+ ......+12

Number of times that will strike

=  2[1+2+3 +....... +12]

S_n  =  (n/2) [a+l]

=  2 ⋅ (12/2) [1+12]

=  12(13)

=  156

So, total number of strikes is 156.

Problem 3 :

Find the sum of the series

400 + 441 + .......... +16000

Solution :

400 + 441 + .......... +16000

=  20² + 21² + ......+40²

(1² + 2² + .......+40²) - (1² + 2² + .......+19²)

Sum of squares  =  n(n+1)(2n+1)/6

  =  40(41)(81)/6 - 15(16)(31)/6

  =  22140 - 1240

  =  22900

Problem 4 :

A circus tent is cylindrical to a height of 3m and conical above it. If the base radius is 52.5 m and slant height of the cone is 53 m, find the area of canvas required to make the tent?

Solution :

Area of canvas  =  πrl

r  =  52.5 m, l  =  53 m

  =  π(52.5) (53)

  =  2782.5π m²

Problem 5 :

In a cultural program 24 students took part in dance 11 in drama, 25 in a group songs, 7 students in dance and drama, 4 students in drama and group songs, 12 students in dance and group songs and 3 participated in all three. If total of 50 students were there in the class,find how many did not participated in the program?

Solution :

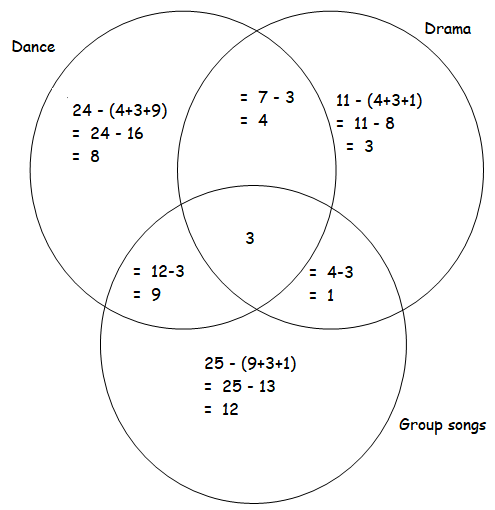
Total number of students  =  50

Number of students participated in any one of the competition  =  8+4+3+3+9+1+12

  =  43

Number of students who did not participate any one of the competition 

  =  50 - 43

  =  7

Problem 6 :

In a triangle ABC m∠C is 20° greater than m∠A. The sum of m∠A and m∠C is twice the m∠B.Find three angles A, B and C. 

Solution :

<C  =  20+<A ---(1)

<A+<C  =  2<B ----(2)

Applying the value of <C in (2), we get

<A+20+<A  =  2<B

2<A - 2<B  =  -20

<B  =  10 + <A

In a triangle, the sum of interior angles of triangle is 180.

<A+<B+<C  =  180

<A+10+<A+20+<A  =  180

3<A + 30  =  180

3<A  =  150

<A  =  50

<B  =  10+50

<B  =  60

<C  =  20+50

<C  =  70

Problem 7 :

A motor boat whose speed is 15 km/hr in still water goes 30 km downstream and comes back in 4 hours 30 minutes.Determine the speed of water. 

Solution :

If the speed of a boat in still water is u km/hr and the speed of the stream is v km/hr, then:

Speed of boat (u)  =  15 km/hr

Speed downstream  =  (u+v) km/hr  =  15 + v

Speed upstream  =  (u-v) km/hr  =  15 - v

Distance to be covered  =  30 km

Time  =  Distance / Speed

30/(15 + v) + 30/(15 - v)  =  4  1/2

30[(15-v+15+v)/225-v²]  =  9/2

30(30)/225-v²  =  9/2

1800  =  9(225-v²)

200  =  225-v²

v²  =  225-200

v  =  5

Speed of water is 5 km/hr.

Problem 8 :

If the points A(2, -2), B(8, 4), C(5, 7) are the vertices of the parallelogram ABCD taken in order, find the fourth vertex D.

Solution :

Midpoint of diagonal AC  =  Midpoint of diagonal BD

Midpoint  =  (x₁ + x₂)/2, (y₁ + y₂)/2

(4 + 8)/2, (6 + 2)/2  =  (10+b)/2, (4 + 4)/2

12/2, 8/2  =  (10+b)/2, 8/2

(6, 4)  =  ((10+b)/2, 4)

Equating x coordinates,

6  =  (10 + b)/2

12  =  10 + b

b  =  12 - 10

b  =  2

So, the value of b is 2.

Problem 9 :

Find the value of a for which the straight lines 2x+y-1 = 0, 2x+ay-3 = 0 and 3x+2y-2 = 0 are concurrent.

Solution :

2x+y-1 = 0 -----(1)

2x+ay-3 = 0 -----(2)

3x+2y-2 = 0 -----(3)

(1) x 2 ==>  4x + 2y - 2 =  0

(1) - (2)     -3x - 2y + 2  =  0

                ---------------------

                       x  =  0

By applying the value of x in (1), we get

0 + y - 1  =  0

y  =  1

The point of intersection of lines is (0, 1).

Since the given lines are concurrent, the other line will pass through the  point (0, 1).

2x+ay-3 = 0

2(0)+a(1)-3  =  0 

a  =  3

So, the value of a is 3.

Problem 10 :

A person stands at a distance of 40 m from a building and observes the top and bottom of a flag pole on the building at angles of elevation 60° and 45°. Find the height of the building and the height of the flag pole.

Solution :

In triangle ABC,

tan ϑ  =  AB/BC

tan 60  =  AB/(40 - x)

√3(40 - x)  =  AB

AB  =  √3(40 - x)-----(1) 

In triangle ABD,

tan 45  =  AB/BD

1  =  AB/40

AB  =  40 -----(2) 

(1)  =  (2)

40  =  √3(40 - x)

40  =  40√3 - x√3

x  =  40(√3 - 1)/√3

x  =  16.90

So, the height of the building is 16.9 m.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.