PROBLEMS ON EXTERIOR ANGLES OF A TRIANGLE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
An exterior angle of a triangle is equal in size to the sum of its interior opposite angles.
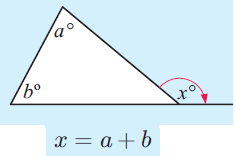
Problem 1 :
In the diagram shown below, find the value of y.
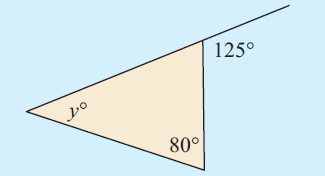
Solution
:
In the triangle above, using Exterior Angle Theorem,
y° + 80° = 125°
y + 80 = 125
Subtract 80 from both sides.
y = 45
Problem 2 :
In the diagram shown below, find the value of x.
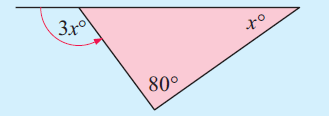
Solution :
In the triangle above, using Exterior Angle Theorem,
x° + 80° = 3x°
x + 80 = 3x
Subtract x from both sides.
80 = 2x
Divide both sides by 2.
40 = x
Problem 3 :
In the diagram shown below, find the values of a and b.
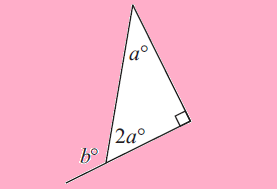
Solution :
In triangle, the sum of interior angles is 180 degrees.
a° + 2a° + 90° = 180°
3a + 90 = 180
Subtract 90 from both sides.
3a = 90
Divide both sides by 3.
a = 30
To find the value of b, we can use any one of the following two ways given below.
|
a + 90 = b 30 + 90 = b 120 = b |
Using linear pair, 2a + b = 180 2(30) + b = 180 60 + b = 180 b = 120 |
In both the ways, the answer will be same.
Problem 4 :
In the diagram shown below, find the value of p.
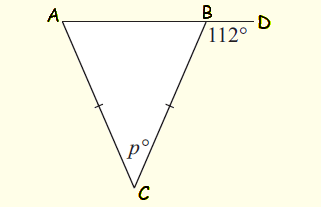
Solution
:
The triangle ABC above is an isosceles triangle.
∠CAB = ∠CBA
∠CBA + ∠CBD = 180°
∠CBA + 112° = 180°
Subtract 112° from both sides.
∠CBA = 68°
In triangle ABC,
∠ACB + ∠CAB + ∠CBA = 180°
p° + 68° + 68° = 180°
p + 136 = 180
Subtract 136 from both side
p = 44
Problem 5 :
In the diagram shown below, find the values of x and y.
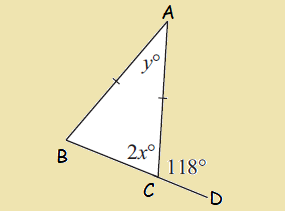
Solution
:
2x° and 118° are linear pair.
2x° + 118° = 180°
Subtract 118 from both sides.
2x = 62
Divide both sides by 2.
x = 31
The given triangle ABC is a isosceles triangle.
∠ABC = ∠ACB = 2x
In triangle ABC,
∠ABC + ∠ACB + ∠CAB = 180°
2x + 2x + y = 180
4x + y = 180
Substitute x = 31.
4(31) + y = 180
124 + y = 180
Subtract 124 from both sides.
y = 56
y = 56
Problem 6 :
Find ∠LMN and ∠MLN.
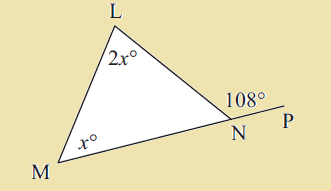
Solution
:
In the triangle above, using Exterior Angle Theorem,
∠LMN + ∠MLN = ∠LNP
x + 2x = 108
3x = 108
Divide both sides by 3.
x = 36
∠LMN = 36°
∠MLN = 2(36°)
∠MLN = 72°
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
