GEOMETRY TERMS AND DEFINITIONS WITH PICTURES

Definition : 

Certain statements are being made in order to create new concepts from the existing without leading to wrong results. Such of the statements are called definitions.

Examples :

1) A triangle is called equilateral if all the sides are of the same length.

2) Two angles are called supplementary if their sum is 180°.

Axiom :

There are certain statements which are assumed to be true. These statements are called axioms.

Examples :

1) There is exactly one and only one straight line passing through two given points.

2) If n is a natural number, then n+1 is also is also a natural number.

Symbol : 

A symbol is nothing but a particular mark which refers to some information.

Some of the symbols and the information indicated by them are given below.

Axiom :

There are certain statements which are assumed to be true. These statements are called axioms.

Examples :

1) There is exactly one and only one straight line passing through two given points.

2) If n is a natural number, then n+1 is also is also a natural number.

Congruence ≅ :

Congruent means equal in all respects or figures whose shapes and sizes are both the same. Now let us discuss about congruent of triangle. 

If the sides and angles of one triangle are equal to the corresponding sides and angles of each other triangle.

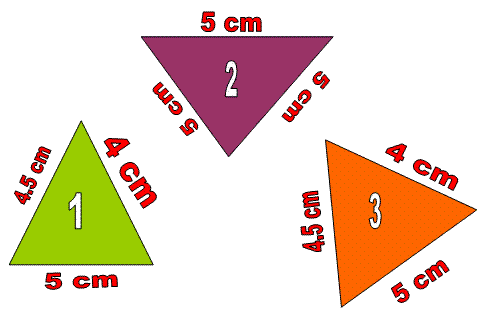
In the above pictures the first and third triangles are congruent to each other. So we can say triangle 1 and triangle 3 are congruent.

Conjecture :

A statement until it is proved or disproved called a conjecture.

Now we are going to see as how a theorem is defined on Geometry dictionary

Theorem :

A conjecture if it is proved becomes a theorem. Thus a statement which has been proved to be true is called theorems. A conjecture, if it is not proven becomes a false statement.

here we can see about points on Geometry dictionary

Point :

A point is used to represent a position in space. In practice, we put a small dot on paper or on a blackboard to indicate a point. But theoretically a point that does not has shape or size. The following Letters A,B,C, and D re the examples of point

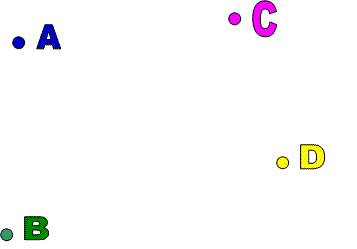
Now we are going to see about lines in Geometry Dictionary

Line :

A set of points that extend infinitely in opposite directions is called a line. We use the symbol. The line has many points.

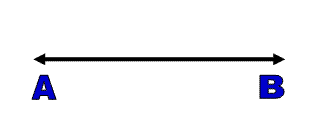
Line segment :

The line segment is a part of the line which is having two end points

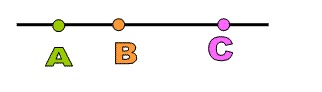
Collinear points :

If three or more points are on a same line, then the points are called collinear points.

Ray :

Ray is nothing but a part of a line with one end point.

Now we are going to look at Angles on Geometry Dictionary

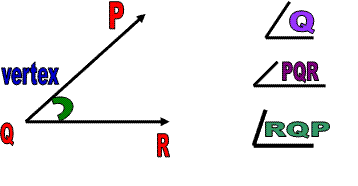
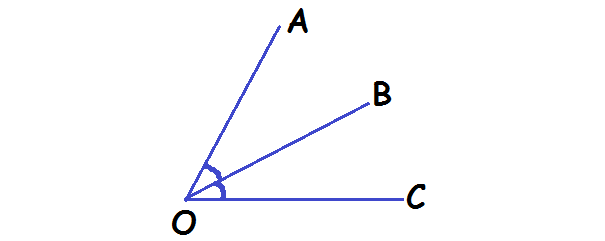
Angle :

The angle is formed by two rays with common end points, called vertex

Angle bisector :

The angle bisector of an angle is the line, which separates the angle. The bisector is nothing but dividing the angle as two equal parts.

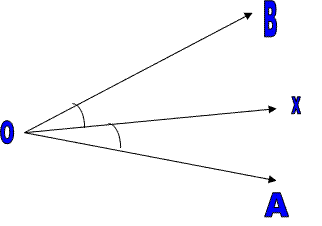
Here OX is the angle bisector of angle BOA Hence angle AOX = angle BOX

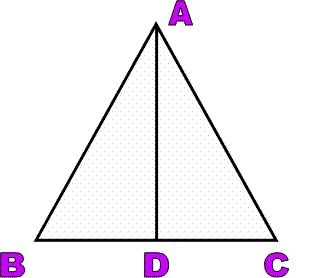
Angle bisector of a triangle :

The angle bisector of any triangle is the line segment which bisects an angle of a triangle Here AD is the angle bisector of triangle ABC.anglebisector.GIF

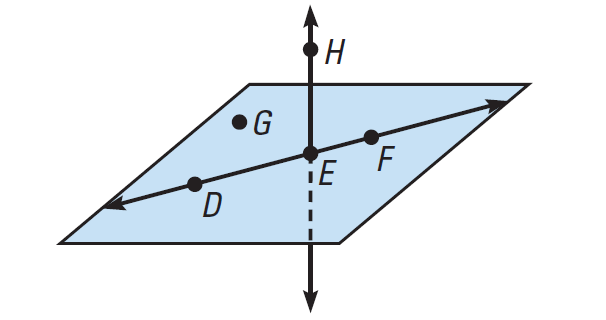
Planes :

Planes are special sets of points. It is a flat surface that extends indefinitely in all directions.

Intersecting of lines :

Intersecting lines are lines that lie in the same plane and meet in a point.

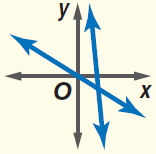
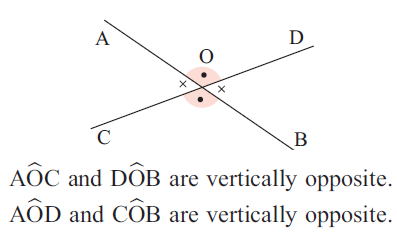
In the above diagram there are two lines intersecting at the point A. This point is called intersection point or point of intersection

Two kinds of angles can be formed when two lines are intersecting.

1) Vertical angle

2) Adjacent angle

Circle :

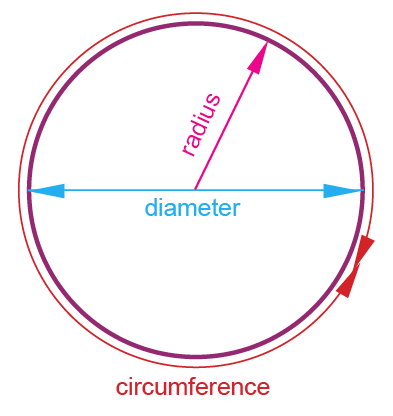
The collection of all the points in the plane, which are which are at a fixed distance from a fixed point in the plane, is called a circle.

Center :

The fixed point is called the center of that particular circle and the fixed distance is called the radius of the circle.

Diameter :

Take any two points on the circle. Here we have taken P and Q The length of PQ is called the diameter of the circle. Diameter divides the circle into two parts (semi circle) Diameter always passing through the center.

Chord :

The line joining any two points on the circumference of a circle is called chord of the circle. It does not pass through the center. Here PQ is called the diameter of the circle and AB is called a chord.

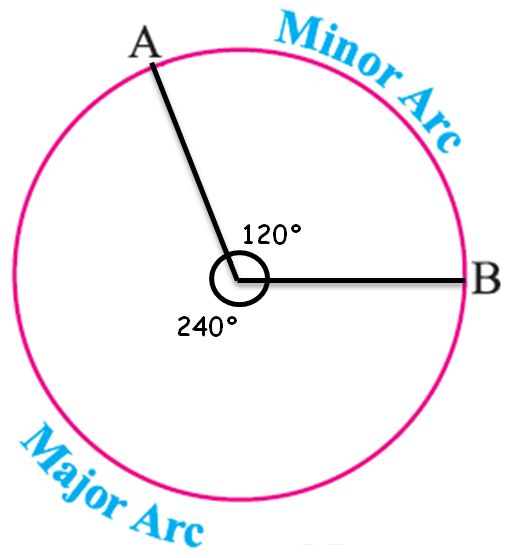
Arc :

A piece of a circle between two points is called an Arc. It can be classified into two parts

1)  Major arc
2)  Minor arc

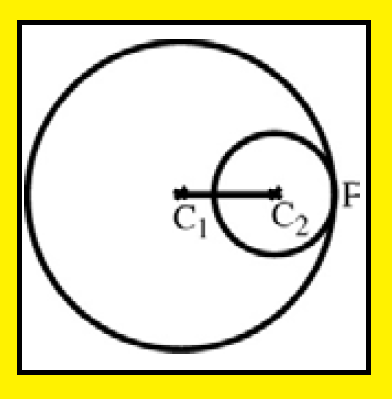
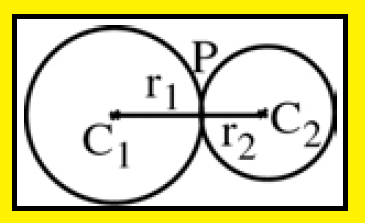
Two circles intersecting in one point :

Two circles are said to touch each other if they should meet at a point and can have a common tangent at this point.

Circles touching externally :

When two circles touch each other, either they will touch each other internally or externally.

We can say two circles touch each other externally when they lie on the opposite sides of the common tangent.

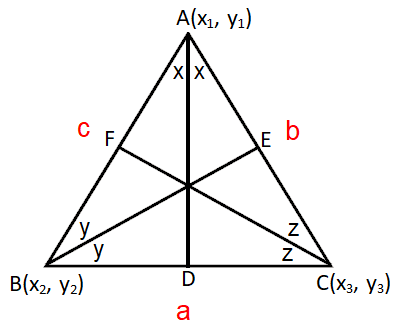
Incenter of a circle :

The point of intersection of the angles of a triangle is called in-center. It is denoted by the letter “I”

Altitude of a Triangle :

The line segment of the perpendicular from a vertex to the opposite side of a triangle is called its altitude.

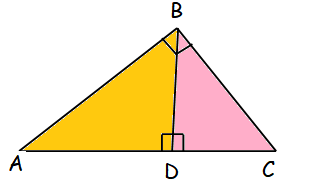
In the above triangle ABC the line AD is perpendicular to the line BC and it produces 90 degrees. So the line AD is called altitude of triangle.

Orthocenter of a triangle :

The point of concurrence of the altitudes from the vertices to the opposite sides of a triangle is called the orthocenter of the triangle.

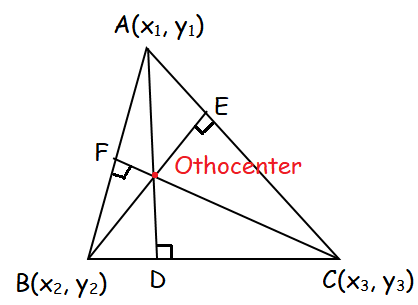
The points of concurrence of all the three altitudes of a triangle are called the orthocenter of the triangle.

Median of a triangle :

A median of the triangle is the line segment that joins a vertex to the midpoint of the opposite side

Here AD is the median of the triangle.

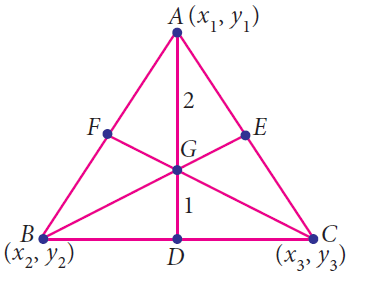
Centroid of the triangle :

The point of the concurrence of the medians of a triangle is called centroid of the triangle.

Here the point G is called centroid of the triangle.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.