GEOMETRIC TERMS AND DEFINITIONS

Points :

We use a point to mark a location or position.

Examples of points are :

(i)  the corner of your desk

(ii)  the tip of your compass needle.

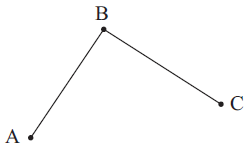
The letters A, B and C identify the points.

Vertices :

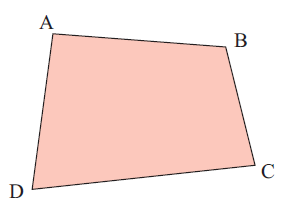
The figure alongside contains four points which have been labelled A, B, C and D. These corner points are also known as vertices.

Straight Line :

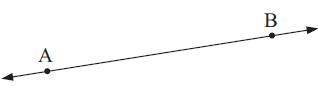
A straight line, usually just called a line, is a continuous infinite collection of points with no beginning or end which lie in a particular direction.

Line segment :

[AB] is the line segment which joins points A and B. We call it “line segment AB” or “line segment BA”. It is only part of the line (AB).

Ray :

[AB) is the ray which starts at A, passes through B, then continues on forever in that direction.

Collinear Points :

If three or more points lie on a single straight line, we say that the points are collinear.

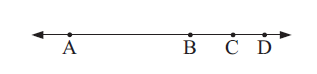
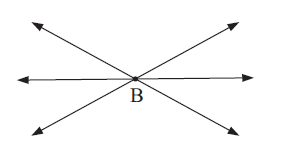
Concurrent lines :

If three or more lines meet or intersect at the same point, we say that the lines are concurrent. The lines shown are concurrent at point B.

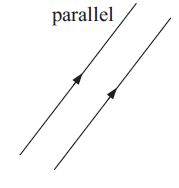
Parallel lines :

Parallel lines are lines which are always a fixed distance apart and never meet.

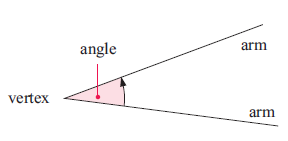
Angle :

An angle is made up of two arms which meet at a point called the vertex.

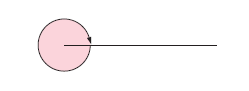
Revolution :

One complete turn. 

One revolution  =  360°

Straight angle :

1/2 turn

1 straight angle  =  180°

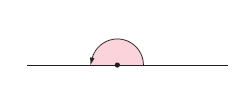
Right angle :

1/4 turn

1 right angle  =  90°

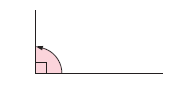
Acute angle :

Less than a 1/4 turn.

An acute angle has size between 0° and 90°.

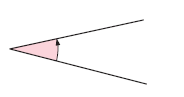
Obtuse angle :

Between 1/4 turn and 1/2 turn.

An obtuse angle has size between 90° and 180°.

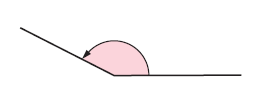
Reflex angle :

Between 1/2 turn and 1 turn.

A reflex angle has size between 180° and 360°.

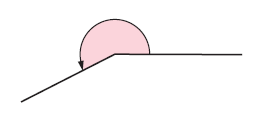
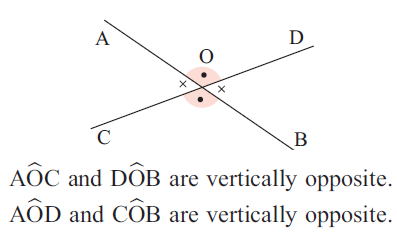
Vertically Opposite Angles :

Vertically opposite angles are formed when two straight lines intersect. The two angles are directly opposite each other through the vertex.

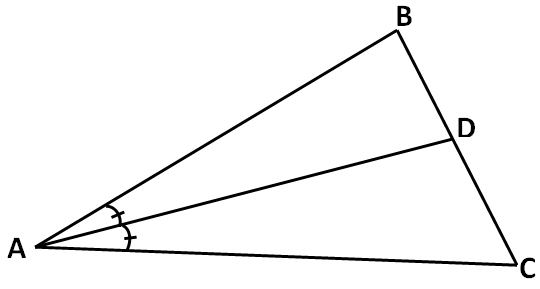
An angle bisector is defined as a ray, segment, or line that divides a given angle into two angles of equal measures.

Angle of elevation :

The angle formed by the line of sight with the horizontal when the object is above the horizontal level is called the angle of elevation.

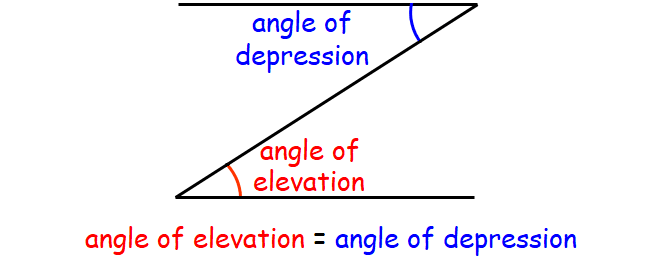
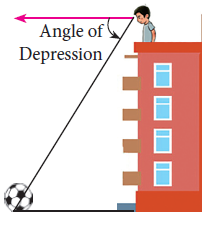
Angle of depression :

The angle formed by the line of sight with the horizontal when the object is below the horizontal level is called the angle of depression.

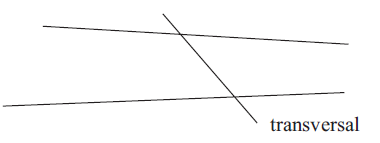
Transversal :

If a third line crosses two other straight lines we call it a transversal.

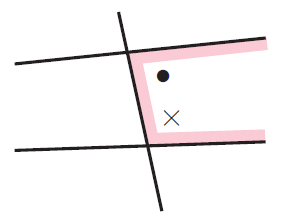
Corresponding Angles :

The angles marked . and "x" are corresponding angles because they are both in the same position. They are on the same side of the transversal and the same side of the two straight lines.

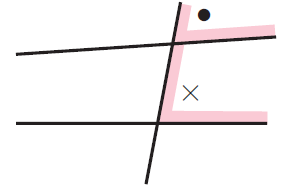
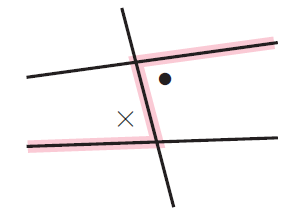
Alternate angle pair :

The angles marked . and x are alternate angles. They are on opposite sides of the transversal and between the two straight lines.

Co interior angle pair :

The angles marked . and x are co-interior angles. They are on the same side of the transversal and between the two straight lines. 

Midpoint :

The midpoint of a line segment is the point that divides the segment into two congruent segments. Congruent segments are segments that have the same length.

You can find the midpoint of a segment by using the coordinates of its endpoints. Calculate the average of the x-coordinates and the average of the y-coordinates of the endpoints.

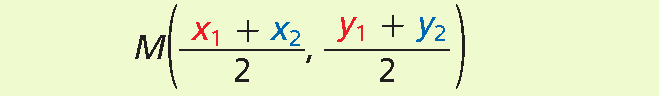
Given two points (x₁, y₁) and (x₂, y₂), the distance between these points is given by the formula

√[(x₂ - x₁)² + (y₂ - y₁)²]

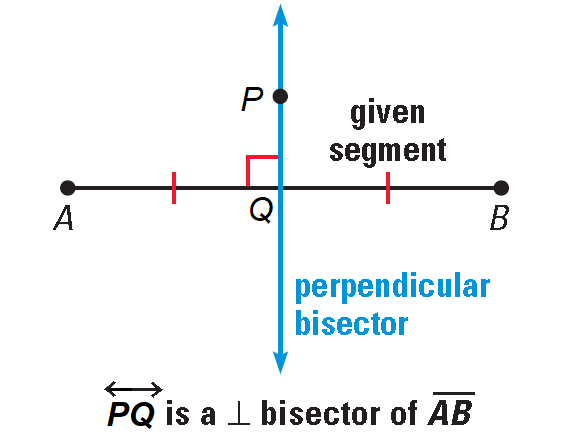
Perpendicular Bisector :

A segment, ray, line, or plane that is perpendicular to another segment at its midpoint is called a perpendicular bisector

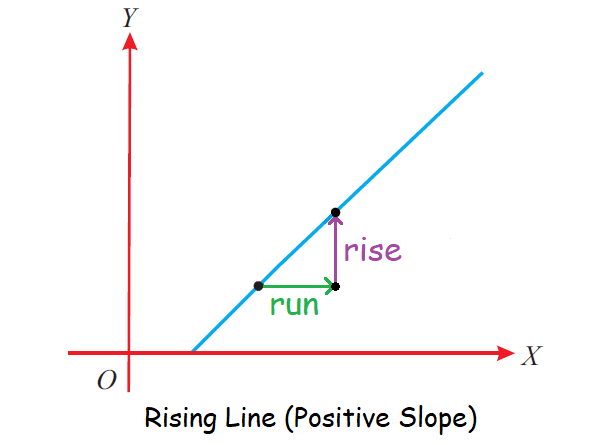
Slope :

The formula for slope is referred to rise over run,

Because the fraction consists of the rise (the change in y, going up or down) divided by the run (the change in x, going from left to the right).

The diagram shown below illustrates this. 

st way to look at the slope is

rise / run

(rise over run)

In the formula (rise / run), we can "rise" up or down... but, we ALWAYS "run" to the right.  

Centroid of triangle :

The centroid of a triangle is the point of concurrency of the medians.

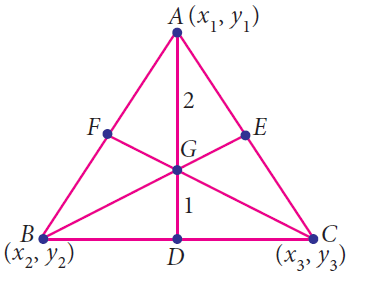
In the above triangle , AD, BE and CF are called medians. All the three medians AD, BE and CF are intersecting at G. So  G is called centroid of the triangle

If the coordinates of A, B and C are (x_1, y₁), (x_2, ,y₂) and (x₃, y₃), then the formula to determine the centroid of the triangle is given by

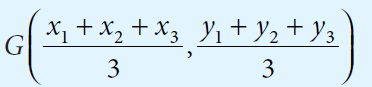
Median of a Triangle

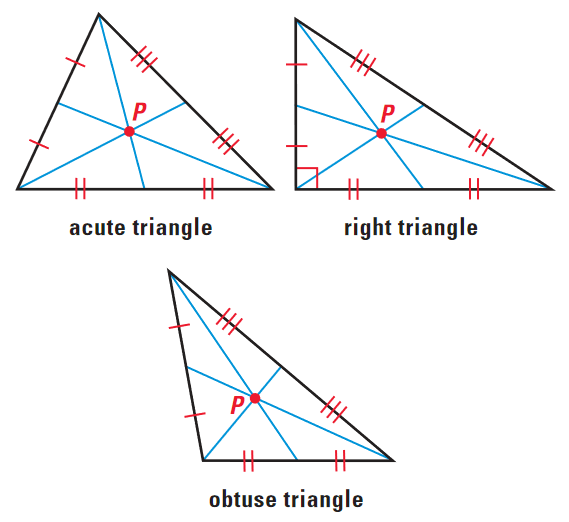
A median of a triangle is a segment whose endpoints are a vertex of the triangle and the midpoint of the opposite side. For instance, in ΔABC shown below, D is the midpoint of side BC. So, AD is the median of the triangle ABC.

The three medians of a triangle are concurrent. The point of concurrency is called the centroid of the triangle. The centroid, labeled P in the diagrams below, is always inside the triangle.

Altitude of a Triangle

An altitude of a triangle is the perpendicular segment from a vertex to the opposite side or to the line that contains the opposite side. An altitude can lie inside, on, or outside the triangle.

Every triangle has three altitudes. The lines containing the altitudes are concurrent and intersect at a point called the orthocenter of the triangle.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.