GEOMETRIC PROBABILITY WORKSHEET

Problem 1 :

Find the probability that a point chosen at random on RS is on TU.

Problem 2 :

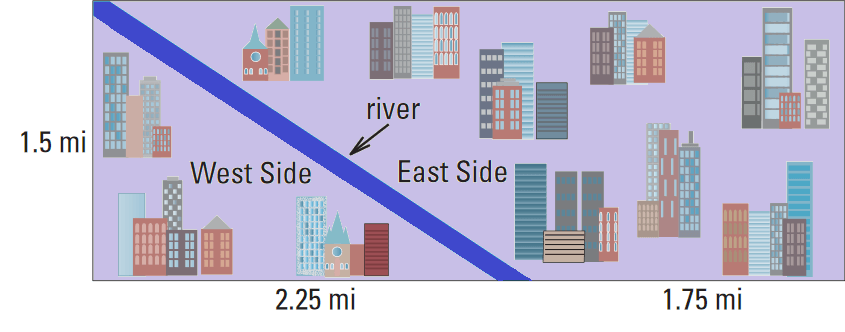
Mr. Johnson works for a temporary employment agency. He lives on the west side of town and prefer to work there. The work assignments are spread evenly throughout the rectangular region shown below. Find the probability that an assignment chosen at random for Mr. Johnson is on the west side of town.

Problem 3 :

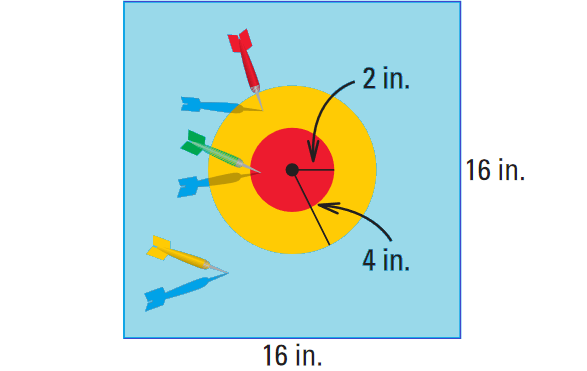
A dart is tossed and hits the dart board shown below. The dart is equally likely to land on any point on the dart board. Find the probability that the dart lands in the red region.

Problem 4 :

Mr. Jacob is visiting San Francisco and taking a trolley ride to a store on Market Street. He is supposed to meet a friend at the store at 3:00 P.M. The trolleys run every 10 minutes and the trip to the store is 8 minutes. Mr. Jacob arrives at the trolley stop at 2:48 P.M. What is the probability that Mr. Jacob will arrive at the store by 3:00 P.M.?

Answers

Problem 1 :

Find the probability that a point chosen at random on RS is on TU.

Answer :

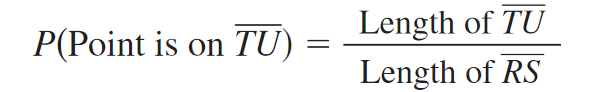
P(Point is on TU)  =  2/10

P(Point is on TU)  = 1/5

So, the probability can be written as 1/5 or 0.2 or 20%.

Problem 2 :

Mr. Johnson works for a temporary employment agency. He lives on the west side of town and prefer to work there. The work assignments are spread evenly throughout the rectangular region shown below. Find the probability that an assignment chosen at random for Mr. Johnson is on the west side of town.

Answer :

The west side of town is approximately triangular. 

Its area is

=  1/2 ⋅ 2.25 ⋅ 1.5

=  1.69 square miles

The area of the rectangular region is

=  1.5 • 4

=  6 square miles

So, the probability that the assignment is on the west side of town is

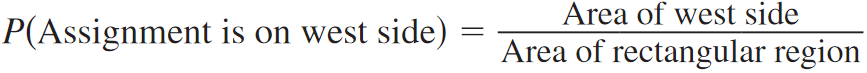
P(Assignment is on west side)  ≈  1.69/6

P(Assignment is on west side)  ≈  0.28

So, the probability that the work assignment is on the west side is about 28%.

Problem 3 :

A dart is tossed and hits the dart board shown below. The dart is equally likely to land on any point on the dart board. Find the probability that the dart lands in the red region.

Answer :

Find the ratio of the area of the red region to the area of the dart board.

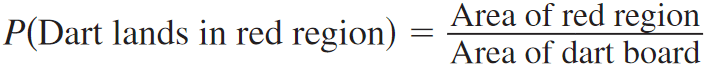
P(Dart lands in red region)  =  π(2)² / 16²

P(Dart lands in red region)  =  4π / 256

Use calculator. 

P(Dart lands in red region)  ≈  0.05

So, the probability that the dart lands in the red region is about 0.05, or 5%.

Problem 4 :

Mr. Jacob is visiting San Francisco and taking a trolley ride to a store on Market Street. He is supposed to meet a friend at the store at 3:00 P.M. The trolleys run every 10 minutes and the trip to the store is 8 minutes. Mr. Jacob arrives at the trolley stop at 2:48 P.M. What is the probability that Mr. Jacob will arrive at the store by 3:00 P.M.?

Answer :

To begin, find the greatest amount of time Mr. Jacob can afford to wait for the trolley and still get to the store by 3:00 P.M. Because the ride takes 8 minutes, he needs to catch the trolley no later than 8 minutes before 3:00 P.M., or in other words by 2:52 P.M. So, Mr. Jacob can afford to wait 4 minutes (2:52 º 2:48 = 4 min). He can use a line segment to model the probability that the trolley will come within 4 minutes.

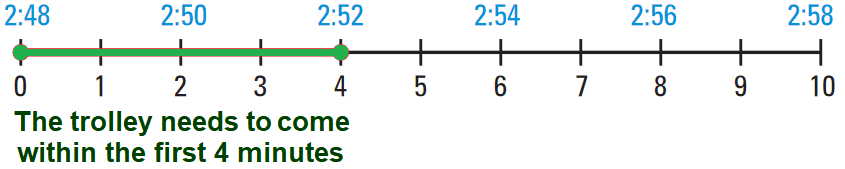
The required probability is

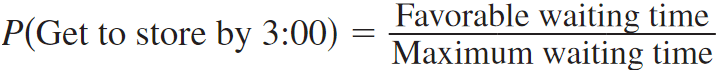
P(Get to store by 3:00)  =  4/10

P(Get to store by 3:00)  =  2/5

So, the probability that Mr. Jacob will arrive at the store by 3:00 P.M. is 2/5 or 0.4 or 40%. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.