GEOMETRIC MEAN THEOREMS

Theorem 1 :

In a right triangle, the length of the altitude dram from the vertex of the right angle to its hypotenuse is the geometric mean between the lengths of the two line segments of the hypotenuse.

Proof :

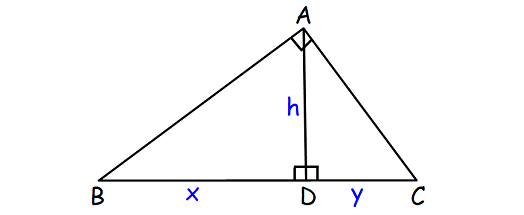
In right triangles DBA and ABC,

∠BAD ≅ ∠BAC (Right Angles)

∠ABD ≅ ∠ABC (Reflexive)

By Angle-Angle Similarity Postulate,

ΔDBA ∼ ΔABC

In right triangles ABC and DAC,

∠BAC ≅ ∠ADC (Right Angles)

∠ACB ≅ ∠ACD (Reflexive)

By Angle-Angle Similarity Postulate,

ΔABC ∼ ΔDAC

ΔDBA ∼ ΔABC and ΔABC ∼ ΔDAC

By Transitive Property,

ΔDBA ∼ ΔDAC

Since the right triangles ABD and ADC are similar, the corresponding sides are proportional.

AD/CD = BD/AD

h/y = x/h

h² = xy

h = √(xy)

Hence, the altitude h is the geometric mean between the lengths of the two line segments x and y of the hypotenuse.

Theorem 2 (without proof) :

In a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments.

The length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the segment of the hypotenuse that is adjacent to the leg.

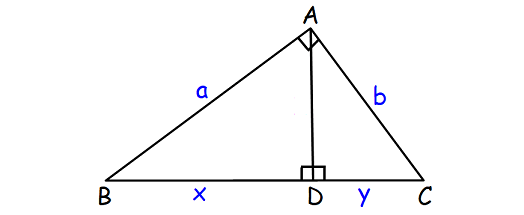
a = √[x(x + y)]

b = √[y(x + y)]

Example 1 :

Find the value x in the triangle shown below.

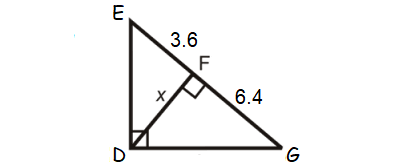
Solution :

EDG is a right triangle and DF is the altitude drawn from the right angle D.

So, DF is the geometric mean between EF and FG.

DF = √(EF ⋅ FG)

x = √(3.6 ⋅ 6.4)

x = √23.04

x = 4.8

Example 2 :

Find the values x and y in the triangle shown below.

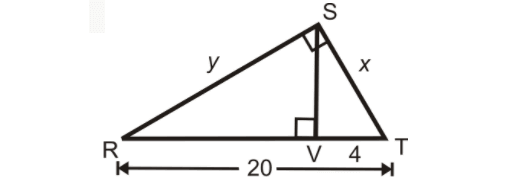
Solution :

RV + VT = RT

RV + 4 = 20

RV = 16

RST is a right triangle and SV is the altitude drawn from the right angle S.

ST is the geometric mean between VT and RT.

ST = √(VT ⋅ RT)

x = √(4 ⋅ 20)

x = √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 5)

x = 2 ⋅ 2 ⋅ √5

x = 4√5

or

x ≈ 8.94

RS is the geometric mean between RV and RT.

RS = √(RV ⋅ RT)

y = √(16 ⋅ 20)

y = √(4 ⋅ 4 ⋅ 2 ⋅ 2 ⋅ 5)

y = 4 ⋅ 2 ⋅ √5

y = 8√5

or

y ≈ 17.89

Example 3 :

Find the value x in the triangle shown below.

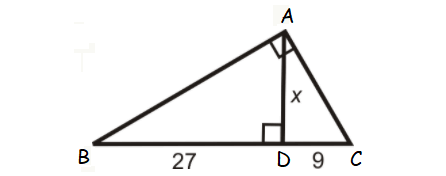
Solution :

ABC is a right triangle and AD is the altitude drawn from the right angle A.

So, AD is the geometric mean between BD and DC.

AD = √(BD ⋅ DC)

x = √(27 ⋅ 9)

x = √(3 ⋅ 9 ⋅ 9)

x = 9√3

or

x ≈ 15.59

Example 4 :

Find the values x and y in the triangle shown below.

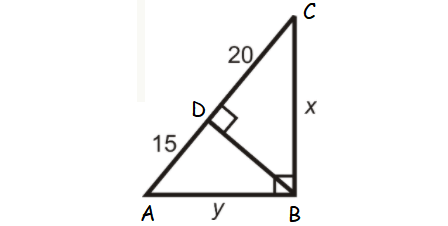
Solution :

AC = AD + DC

AC = 15 + 20

AC = 35

ABC is a right triangle and BD is the altitude drawn from the right angle B.

So, BC is the geometric mean between CD and AC.

BC = √(CD ⋅ AC)

x = √(20 ⋅ 35)

x = √(2 ⋅ 2 ⋅ 5 ⋅ 5 ⋅ 7)

x = 2 ⋅ 5 ⋅ √7

x = 10√7

or

x ≈ 26.46

So, AB is the geometric mean between AD and AC.

AB = √(AD ⋅ AC)

y = √(15 ⋅ 35)

y = √(3 ⋅ 5 ⋅ 5 ⋅ 7)

x = 5√(3 ⋅ 7)

x = 5√21

or

x ≈ 22.91

Example 5 :

Find the value y in the triangle shown below.

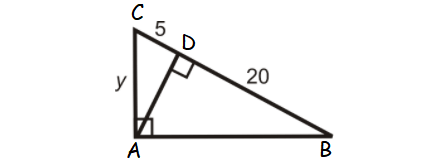
Solution :

ABC is a right triangle and AD is the altitude drawn from the right angle A.

So, AC is the geometric mean between CD and BC.

AC = √(CD ⋅ BC)

y = √(5 ⋅ 25)

y = √(5 ⋅ 5 ⋅ 5)

y = 5√5

or

y ≈ 11.18

Example 6 :

Find the value x in the triangle shown below.

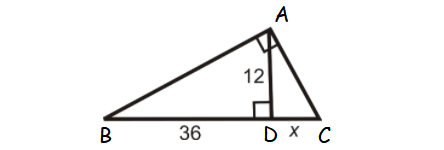
Solution :

ABC is a right triangle and AD is the altitude drawn from the right angle A.

So, AD is the geometric mean between BD and DC.

AD = √(BD ⋅ DC)

12 = √(36 ⋅ x)

12² = 36x

144 = 36x

Divide both sides by 36.

4 = x

Example 7 :

Find the value z in the triangle shown below.

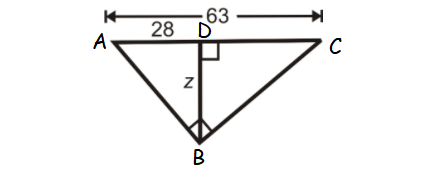
Solution :

AD + DC = AC

28 + DC = 63

DC = 35

ABC is a right triangle and BD is the altitude drawn from the right angle B.

So, BD is the geometric mean between AD and DC.

BD = √(AD ⋅ DC)

z = √(28 ⋅ 35)

z = √(2 ⋅ 2 ⋅ 7 ⋅ 7 ⋅ 5)

z = 2 ⋅ 7 ⋅ √5

z = 14√5

or

z ≈ 31.30

Example 8 :

Find the values x, y and z in the triangle shown below.

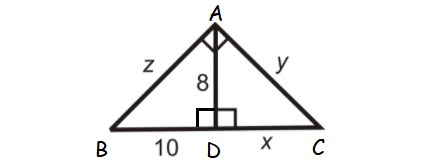
Solution :

In right triangle ABD,

z² = 10² + 8²

z² = 164

z = √164

z = √(2 ⋅ 2 ⋅ 41)

Take square root on both sides.

z = 2√41

or

z ≈ 12.81

ABC is a right triangle and AD is the altitude drawn from the right angle A.

So, AD is the geometric mean between BD and DC.

AD = √(BD ⋅ DC)

8 = √(10 ⋅ x)

Raise to the power of 2 on both sides.

8² = 10x

64 = 10x

Divide both sides by 10.

6.4 = x

In right triangle ACD,

y² = x² + 8²

Substitute x = 6.4.

y² = 6.4² + 8²

y² = 40.96 + 64

y² = 104.96

Take square root on both sides.

y = √104.96

y ≈ 10.24

Example 9 :

Find the values x and y in the triangle shown below.

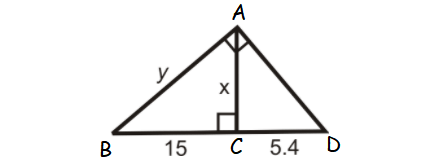
Solution :

ABD is a right triangle and AC is the altitude drawn from the right angle A.

So, AC is the geometric mean between BC and CD.

AC = √(BC ⋅ CD)

x = √(15 ⋅ 5.4)

x = √81

x = 9

In right triangle ABC,

y² = x² + 15²

Substitute x = 9.

y² = 9² + 15²

y² = 81 + 225

y² = 306

Take square root on both sides.

y = √306

y = √(3 ⋅ 3 ⋅ 2 ⋅ 17)

y = 3√(2 ⋅ 17)

y = 3√34

or

y ≈ 17.49

Example 10 :

Find the values x, y and z in the triangle shown below.

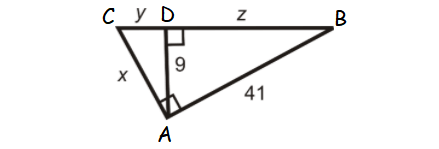
Solution :

In right triangle ABB,

41² = 9² + z²

1681 = 81 + z²

Subtract 81 from both sides.

1600 = z²

Take square root on both sides.

40 = z

ABC is a right triangle and AD is the altitude drawn from the right angle A.

So, AD is the geometric mean between CD and DB.

AD = √(CD ⋅ DB)

9 = √(y ⋅ z)

Substitute z = 40.

9 = √(y ⋅ 40)

Raise to the power of 2 on both sides.

9² = 40y

81 = 40y

Divide both sides by 40.

2.025 = y

In right triangle ACD,

x² = 9² + y²

Substitute y = 2.025.

x² = 9² + 2.025²

x² = 81 + 4.100625

x² = 85.100625

Take square root on both sides.

x = 9.225

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.