GEOMETRIC MEAN IN RIGHT TRIANGLES WORKSHEET

Question 1 :

Find the value x in the triangle shown below.

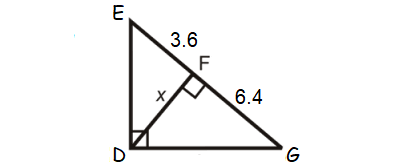
Question 2 :

Find the values x and y in the triangle shown below.

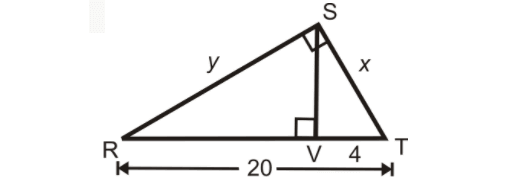
Question 3 :

Find the value x in the triangle shown below.

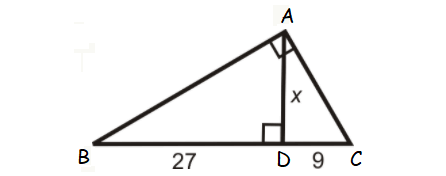
Question 4 :

Find the values x and y in the triangle shown below.

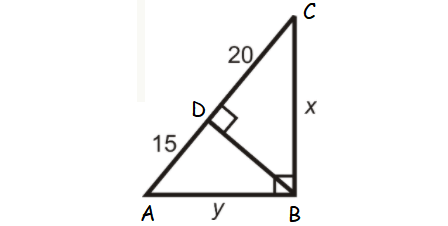
Question 5 :

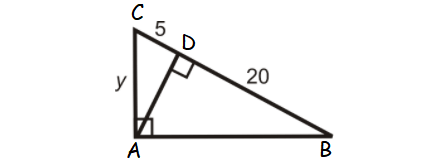
Find the value y in the triangle shown below.

Question 6 :

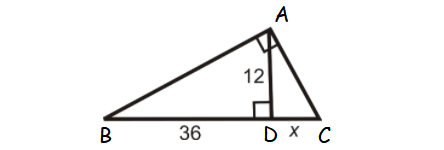
Find the value x in the triangle shown below.

Question 7 :

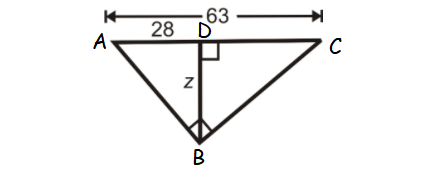
Find the value z in the triangle shown below.

Question 8 :

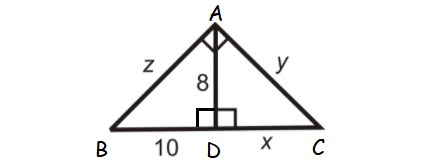
Find the values x, y and z in the triangle shown below.

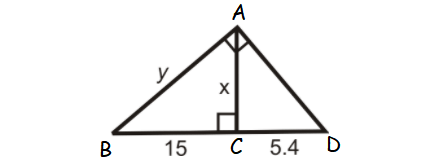
Question 9 :

Find the values x and y in the triangle shown below.

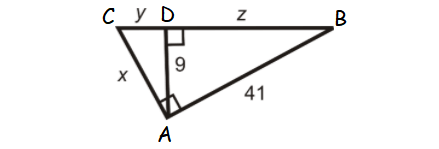
Question 10 :

Find the values x, y and z in the triangle shown below.

Answers

1. Answer :

EDG is a right triangle and DF is the altitude drawn from the right angle D.

So, DF is the geometric mean between EF and FG.

DF = √(EF ⋅ FG)

x = √(3.6 ⋅ 6.4)

x = √23.04

x = 4.8

2. Answer :

RV + VT = RT

RV + 4 = 20

RV = 16

RST is a right triangle and SV is the altitude drawn from the right angle S.

ST is the geometric mean between VT and RT.

ST = √(VT ⋅ RT)

x = √(4 ⋅ 20)

x = √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 5)

x = 2 ⋅ 2 ⋅ √5

x = 4√5

or

x ≈ 8.94

RS is the geometric mean between RV and RT.

RS = √(RV ⋅ RT)

y = √(16 ⋅ 20)

y = √(4 ⋅ 4 ⋅ 2 ⋅ 2 ⋅ 5)

y = 4 ⋅ 2 ⋅ √5

y = 8√5

or

y ≈ 17.89

3. Answer :

ABC is a right triangle and AD is the altitude drawn from the right angle A.

So, AD is the geometric mean between BD and DC.

AD = √(BD ⋅ DC)

x = √(27 ⋅ 9)

x = √(3 ⋅ 9 ⋅ 9)

x = 9√3

or

x ≈ 15.59

4. Answer :

AC = AD + DC

AC = 15 + 20

AC = 35

ABC is a right triangle and BD is the altitude drawn from the right angle B.

So, BC is the geometric mean between CD and AC.

BC = √(CD ⋅ AC)

x = √(20 ⋅ 35)

x = √(2 ⋅ 2 ⋅ 5 ⋅ 5 ⋅ 7)

x = 2 ⋅ 5 ⋅ √7

x = 10√7

or

x ≈ 26.46

So, AB is the geometric mean between AD and AC.

AB = √(AD ⋅ AC)

y = √(15 ⋅ 35)

y = √(3 ⋅ 5 ⋅ 5 ⋅ 7)

x = 5√(3 ⋅ 7)

x = 5√21

or

x ≈ 22.91

5. Answer :

ABC is a right triangle and AD is the altitude drawn from the right angle A.

So, AC is the geometric mean between CD and BC.

AC = √(CD ⋅ BC)

y = √(5 ⋅ 25)

y = √(5 ⋅ 5 ⋅ 5)

y = 5√5

or

y ≈ 11.18

6. Answer :

ABC is a right triangle and AD is the altitude drawn from the right angle A.

So, AD is the geometric mean between BD and DC.

AD = √(BD ⋅ DC)

12 = √(36 ⋅ x)

12² = 36x

144 = 36x

Divide both sides by 36.

4 = x

7. Answer :

AD + DC = AC

28 + DC = 63

DC = 35

ABC is a right triangle and BD is the altitude drawn from the right angle B.

So, BD is the geometric mean between AD and DC.

BD = √(AD ⋅ DC)

z = √(28 ⋅ 35)

z = √(2 ⋅ 2 ⋅ 7 ⋅ 7 ⋅ 5)

z = 2 ⋅ 7 ⋅ √5

z = 14√5

or

z ≈ 31.30

8. Answer :

In right triangle ABD,

z² = 10² + 8²

z² = 164

z = √164

z = √(2 ⋅ 2 ⋅ 41)

Take square root on both sides.

z = 2√41

or

z ≈ 12.81

ABC is a right triangle and AD is the altitude drawn from the right angle A.

So, AD is the geometric mean between BD and DC.

AD = √(BD ⋅ DC)

8 = √(10 ⋅ x)

Raise to the power of 2 on both sides.

8² = 10x

64 = 10x

Divide both sides by 10.

6.4 = x

In right triangle ACD,

y² = x² + 8²

Substitute x = 6.4.

y² = 6.4² + 8²

y² = 40.96 + 64

y² = 104.96

Take square root on both sides.

y = √104.96

y ≈ 10.24

9. Answer :

ABD is a right triangle and AC is the altitude drawn from the right angle A.

So, AC is the geometric mean between BC and CD.

AC = √(BC ⋅ CD)

x = √(15 ⋅ 5.4)

x = √81

x = 9

In right triangle ABC,

y² = x² + 15²

Substitute x = 9.

y² = 9² + 15²

y² = 81 + 225

y² = 306

Take square root on both sides.

y = √306

y = √(3 ⋅ 3 ⋅ 2 ⋅ 17)

y = 3√(2 ⋅ 17)

y = 3√34

or

y ≈ 17.49

10. Answer :

In right triangle ABB,

41² = 9² + z²

1681 = 81 + z²

Subtract 81 from both sides.

1600 = z²

Take square root on both sides.

40 = z

ABC is a right triangle and AD is the altitude drawn from the right angle A.

So, AD is the geometric mean between CD and DB.

AD = √(CD ⋅ DB)

9 = √(y ⋅ z)

Substitute z = 40.

9 = √(y ⋅ 40)

Raise to the power of 2 on both sides.

9² = 40y

81 = 40y

Divide both sides by 40.

2.025 = y

In right triangle ACD,

x² = 9² + y²

Substitute y = 2.025.

x² = 9² + 2.025²

x² = 81 + 4.100625

x² = 85.100625

Take square root on both sides.

x = 9.225

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.