GEOMETRIC DRAWINGS

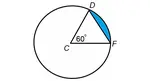
Drawing Three Sides

Use geometry software to draw a triangle whose sides have the following lengths: 2 units, 3 units, and 4 units.

Step 1 :

Draw the segments. 

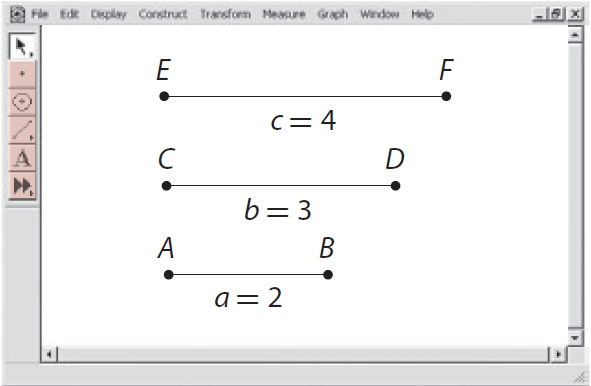
Step 2 :

Let AB be the base of the triangle. Place point C on top of point B and point E on top of point A.

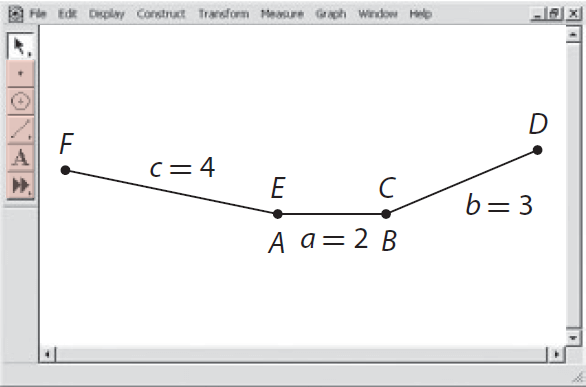
Step 3 :

Using the points C and E as fixed vertices, rotate points F and D to see if they will meet in a single point.

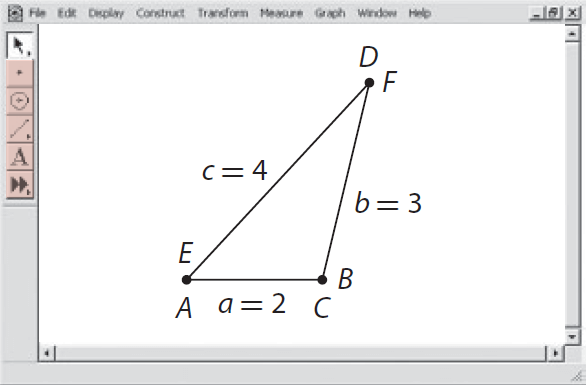
Note that the line segments form a triangle.

Question 1 :

Repeat step 1 and step 2, but use a different segment as the base. Do the segments form a triangle? If so, is it the same as the original triangle ?

Answer :

Yes; the triangle has the same size and shape as the original.

Question 2 :

Use geometry software to draw a triangle with sides of length 2, 3, and 6 units, and one with sides of length 2, 3, and 5 units. Do the line segments form triangles? How does the sum of the lengths of the two shorter sides of each triangle compare to the length of the third side ?

Answer :

1 st  :  no, 2 + 3 < 6

2 nd  :  no; 2 + 3  =  5

Question 3 : 

Do two segments of lengths a and b units and a longer segment of length c units form one triangle, more than one, or none ?

Answer :

One triangle if a + b > c ; none if a + b ≤ c.

Two Angles and Their Included Side

Use a ruler and a protractor to draw a triangle for the given measures.

Angles : 30° and 80°

Length of included side : 2 inches

Step 1 :

Use a ruler to draw a line that is 2 inches long. This will be the included side.

Step 2 :

Place the center of the protractor on the left end of the 2-in. line. Then make a 30°-angle mark.

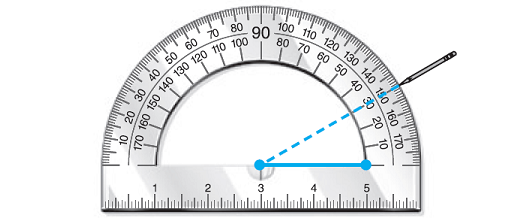
Step 3 :

Draw a line connecting the left side of the 2-in. line and the 30°-angle mark. This will be the 30° angle.

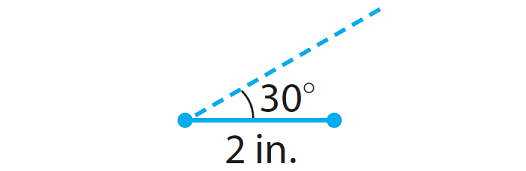
Step 4 :

Repeat Step 2 on the right side of the triangle to construct the 80° angle.

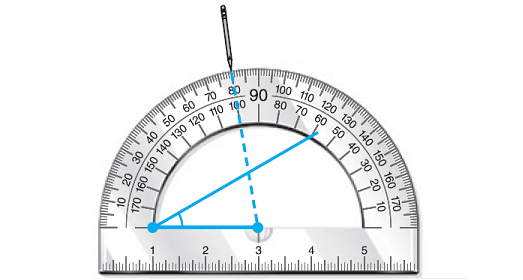
Step 5 :

The side of the 80° angle and the side of the 30° angle will intersect. This is Triangle 1 with angles of 30° and 80° and an included side of 2 inches.

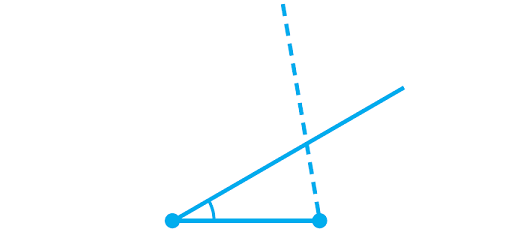
Question 4 :

Will a triangle be unique if you know all three angle measures but no side lengths ?

Answer :

Yes, the two angles and the length of the included side determine the point at which the sides meet. The triangle is unique.

Question 5 :

What quadrilaterals can you draw that have exactly four right angles ?

Answer :

Quadrilateral will have four sides and four angles. When the quadrilateral which has four right angles is called rectangle.

Question 6 :

What quadrilateral can you draw that has exactly one pair of parallel sides ?

Answer :

The quadrilateral which has exactly one pair of parallel sides is known as trapezium.

Question 7 :

What quadrilateral can you draw that they have two side lengths of 9 cm and two side length of 4 cm ?

Answer :

Two sides which has the measure 9 cm and other two sides which has the measure of 4 cm.

From this information, the opposite sides are parallel. Then this shape is known as parallelogram. There is no right angle which is given so, it cannot be a rectangle.

Question 8 :

A four sided sandbox has more than two right angles, two side of lengths of 2 feet and two side lengths of 5 feet. What geometric shape best describes the shape of the sandbox ?

Answer :

The four sided shape which has more than two right angles.

Two sides which has the length of 2 feet and other two sides which has the length of 5 feet. Since opposite sides are equal, then it must be a rectangle.

Question 9 :

A friend is building a 4 sided garden with two side lengths of 19 feet and exactly one right angle. What quadrilaterals could describe the garden ?

Answer :

Two sides which has the measure of 19 feet and exactly one right angle. This may be a quadrilateral with one right angle.

Question 10 :

An engineer makes a scale drawing of the floor of a building. The floor has two pairs of parallel sides that are 50 feet and 80 feet. Two of four angle measures 60 degree. Make the scale drawing, what is the name of the floor's shape ?

Answer :

Step 1 :

Draw two line segments at a 60 degree angle using a scale of 1 unit = 10 feet, the segments should be 5 units and 8 units long.

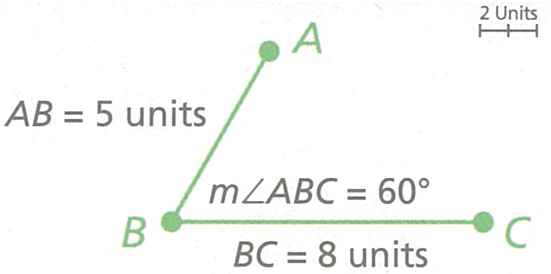
Step 2 :

Duplicate each line segment to create pairs of parallel sides and move them to construct a closed figure.

The floor shape is in the shape of parallelogram.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.