GENERATING EQUIVALENT EXPRESSIONS

An algebraic expression is a mathematical sentence involving constants (any real number), variables and the algebraic operations (addition, subtraction, multiplication, division and exponentiation by an exponent that is a rational number).

To generate equivalent expression to another expression, we have to be aware of the parts of an algebraic expression. 

We can use properties to combine like terms in an expression.

For example, let us consider the algebraic expression

3x + 2x + 4

You can  add / subtract the coefficients of the like terms to combine them. 

3x + 2x + 4  =  5x + 4

Write the equivalent expressions for the following :

Example 1 :

6x² - 4x²

Solution :

= 6x² - 4x²

= 2x²

Example 2 :

-3(5 - 6x)

Solution :

= -3(5 - 6x)

Use Distributive Property. 

= -3(5) - 3(-6x)

= -15 + 18x

= 18x - 15

Example 3 :

3a + 2(b + 5a)

Solution :

= 3a + 2(b + 5a)

Use Distributive Property. 

= 3a + 2b + 2(5a)

= 3a + 2b + 10a

= 13a + 2b

Example 4 :

 y + 11x + 7y - 7x

Solution :

= y + 11x + 7y - 7x

= 4x + 8y

Example 5 :

8m + 14 - 12 + 4n

Solution :

= 8m + 14 - 12 + 4n

= 8m + 4n + 2

Example 6 :

7(x - 3) + 2(2x - 5) - 3(x - 5)

Solution :

= 7(x - 3) + 2(2x - 5) - 3(x - 5)

Use Distributive Property.

= 7(x) + 7(-3) + 2(2x) + 2(-5) - 3(x) - 3(-5)

= 7x - 21 + 4x - 10 - 3x + 15

= 8x - 16

Example 7 :

4x - (2 + 4x) - 2(x - 1) - 8(x -3)

Solution :

= 4x - (2 + 4x) - 2(x - 1) - 8(x -3)

Use Distributive Property.

= 4x - 2 - 4x - 2(x) - 2(-1) - 8(x) - 8(-3)

= 4x - 2 - 4x - 2x + 2 - 8x + 24

= -10x + 24

Example 8 :

(x + 3)² - (x - 3)²

Solution :

= (x + 3)² - (x - 3)²

= (x + 3)(x + 3) - (x - 3)(x - 3)

= (x² + 3x + 3x + 9) - (x² - 3x - 3x + 9)

= (x² + 6x + 9) - (x² - 6x + 9)

= x² + 6x + 9 - x² + 6x - 9

= 12x

Example 9 :

x² + 5x - (x + 3)(x - 3)

Solution :

= x² + 5x - (x + 3)(x - 3)

= x² + 5x - (x² - 3x + 3x - 9)

= x² + 5x - (x² - 9)

= x² + 5x - x² + 9

= 5x + 9

Example 10 :

25(x + 5) - 5(x + 5)²

Solution :

= 25(x + 5) - 5(x + 5)²

Factor (x + 5).

= (x + 5)[25 - 5(x + 5)]

= (x + 5)(25 - 5x + 25)

= (x + 5)(-5x)

= x(-5x) + 5(-5x)

= -5x² - 25x

Find the value of x that makes the expressions equivalent.

Example 11 :

4(x − 5); 32 − 20

Solution :

4(x − 5) = 32 − 20

Using distributive property, we get

4x - 20 = 12

4x = 12 + 20

4x = 32

x = 32/4

x = 8

Example 12 :

2(x + 9); 30 + 18

Solution :

2(x + 9) = 30 + 18

Using distributive property, we get

2x + 18 = 48

2x = 48 - 18

2x = 30

x = 30/2

x = 15

Example 13 :

7(8 − x); 56 − 21

Solution :

7(8 − x) = 56 − 21

Using distributive property, we get

56 - 7x = 35

-7x = 35 - 56

-7x = -21

x = 21/7

x = 3

Example 14 :

Simplify the expressions and compare. What do you notice? Explain.

Column A : 4(x + 6)

Column B : (x + 6) + (x + 6) + (x + 6) + (x + 6)

Solution :

Column A :

= 4(x + 6)

= 4x + 4(6)

= 4x + 24

Column B :

= (x + 6) + (x + 6) + (x + 6) + (x + 6)

= x + x + x + x + 6 + 6 + 6 + 6

= 4 x + 24

Example 15 :

The area of the parallelogram is (4x + 16) square feet. Write an expression for the base

Solution :

Area of the parallelogram = (4x + 16) square feet

Height = 4 ft

Area of parallelogram = base ⋅ height

4x + 16 = base ⋅ 4

base = (4x + 16)/4

= 4x/4 + 16/4

= (x + 4) ft

Example 16 :

The expression 18 + 7 + (18 + 2x) + 7 represents the perimeter of the trapezoid. Simplify the expression

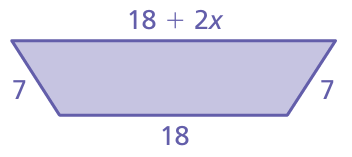
Solution :

Perimeter of trapezoid = 18 + 7 + (18 + 2x) + 7

= 25 + 18 + 2x + 7

= 25 + 18 + 7 + 2x

= 50 + 2x

So, perimeter of the trapezoid is 50 + 2x ft.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.