GCF AND LCM WORD PROBLEMS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
The sum of two numbers is 588 and their greatest common factor (GCF) is 49. How many such pairs of numbers can be formed ?
Solution :
Because the GCF 49, the two numbers can be assumed as 49x and 49y.
Their sum is 588. Then,
49x + 49y = 588
Divide each side 49.
x + y = 12
We have to find the values of x and y such that their sum is 12.
The possible pairs of values of (x, y) are
(1, 11), (2, 10), (3, 9), (4, 8), (5, 7), (6, 6)
In the above pairs of values, only co-primes will meet the condition given in the question.
[Co-primes = Two integers are said to be co-primes or relatively prime if they have no common positive factor other than 1 or, equivalently, if their greatest common divisor is 1].
In the above pairs, (1, 11) and (5, 7) are the co-primes.
Hence, the number of pairs is 2.
Problem 2 :
The product of two numbers is 2028 and their greatest common factor (GCF) is 13. Find the number of such pairs.
Solution :
Since the GCF is 13, the two numbers could be 13x and 13y.
Their product is 2028. Then
(13x) ⋅ (13y) = 2028
169xy = 2028
Divide each side by 169.
xy = 12
We have to find the values of x and y such that their product is 12.
The possible pairs of values of (x, y) are
(1, 12), (2, 6), (3, 4)
In the above pairs of values, only co-primes will meet the condition given in the question.
In the above pairs, (1, 12) and (3, 4) are the co-primes.
Hence, the number of pairs is 2.
Problem 3 :
Lenin is preparing dinner plates. He has 12 pieces of chicken and 16 rolls. If he wants to make all the plates identical without any food left over, what is the greatest number of plates Lenin can prepare ?
Solution :
To make all the plates identical and find the greatest number of plates, we have to find the greatest number that can divide 12 and 16 evenly. That is the highest common factor of 12 and 16.
GCF (12, 16) = 4
That is, 12 pieces of chicken would be served in 4 plates at the rate of 3 pieces per plate.
And 16 rolls would be served in 4 plates at the rate of 4 rolls per plate.
In this way, each of the 4 plates would have 3 pieces of chicken and 4 rolls. And all the 4 plates would be identical.
Hence, the greatest number of plates Lenin can prepare is 4
Problem 4 :
The drama club meets in the school auditorium every 2 days, and the choir meets there every 5 days. If the groups are both meeting in the auditorium today, then how many days from now will they next have to share the auditorium ?
Solution :
If the drama club meets today, again they will meet after 2, 4, 6, 8, 10, 12.... days.
Like this, if the choir meets today, again they will meet after 5, 10, 15, 20 .... days.
From the explanation above, If both drama club and choir meet in the auditorium today, again, they will meet after 10 days.
And also, 10 is the least common multiple of (2, 5).
Hence, both the groups will share the auditorium after ten days.
Problem 5 :
John is printing orange and green forms. He notices that 3 orange forms fit on a page, and 5 green forms fit on a page. If John wants to print the exact same number of orange and green forms, what is the minimum number of each form that he could print ?
Solution :
The condition of the question is, the number of orange forms taken must be equal to the number of green forms taken.
Let us assume that he takes 10 orange and 10 green forms.
10 green forms can be fit exactly on 2 pages at 5 forms/page. But,10 orange forms can't be fit exactly on any number of pages.
Because, 3 orange forms can be fit exactly on a page. In 10 orange forms, 9 forms can be fit exactly on 3 pages and 1 form will be remaining.
To get the number of forms in orange and green which can be fit exactly on some number of pages, we have to find the least common multiple of (3, 5).
LCM (3, 5) = 15
15 orange forms can be fit exactly on 5 pages at 3 forms/page.
15 green forms can be fit exactly on 3 pages at 5 forms/page.
Hence, the smallest number of each form could be printed is 15.
Problem 6 :
In two numbers, one number is a multiple of 6 and the other one is a multiple of 7. If their LCM is 84, then find the two numbers.
Solution :
From the given information, the numbers can be assumed as 6x and 7x.
We can find LCM of 6x and 7x using synthetic division as given below.
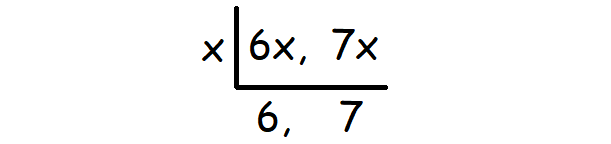
Therefore, LCM of (6x, 7x) is
= x ⋅ 6 ⋅ 7
= 42x
Given : LCM of the two numbers is 84.
Then,
42x = 84
Divide each side by 42.
x = 2
Substitute 2 for x in 6x and 7x.
6x = 6 ⋅ 2 = 12
7x = 7 ⋅ 2 = 14
So, the two numbers are 12 and 14.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 43)
Jan 04, 26 01:38 AM
10 Hard SAT Math Questions (Part - 43) -
90 Degree Clockwise Rotation
Jan 01, 26 06:58 AM
90 Degree Clockwise Rotation - Rule - Examples with step by step explanation -
US Common Core K-12 Curriculum Algebra Solving Systems of Equations
Jan 01, 26 04:51 AM
US Common Core K-12 Curriculum - Algebra : Solving Systems of Linear Equations
