GCF AND LCM WORD PROBLEMS WORKSHEET

1) Lily has collected 8 U.S. stamps and 12 international stamps. She wants to display them in identical groups of U.S. and international stamps, with no stamps left over. What is the greatest number of groups Lily can display them in ?

2) Jill wants to put 45 sunflower plants, 81 corn plants, and 63 tomato plants in her garden. If she puts the same number of plants in each row and if each row has only one type of plant, what is the greatest number of plants Jill can put in one row ?

3) Two numbers are in the ratio 6 : 7 and their greatest common factor (GCF) is 13. Find the numbers. 

4) In a clock, a large gear completes a rotation every 45 seconds, and a small gear completes a rotation every 18 seconds. If the gears are aligned now, how many seconds will pass before the gears are aligned again ?

5) Dante is planting his rose garden. He knows he can plant all of his roses by planting 12 or 15 rose bushes in every row. What is the least number of rose bushes Dante could have ?

6) Two numbers are in the ratio 5 : 9. If the second number is 72, find their least common multiple.

Detailed Answer Key

Answer (1) : 

To make all the groups identical and find the greatest number of groups, we have to find the greatest number which can divide 8 and 12 exactly. That is the greatest common factor of (GCF) of 8 and 12.

GCF (8, 12)  =  4

That is, 8 U.S stamps can be displayed in 4 groups at 2 stamps/group.

And 12 international stamps can be displayed in 4 groups at 3 stamps/group.

In this way, each of the 4 groups would have 2 U.S stamps and 3 international stamps. And all the 4 groups would be identical.

Hence, the greatest number of groups can be made is 4.

Answer (2) : 

To put the same number of plants in each row and if each row has only one type of plant, we have to find the greatest number that can evenly divide 45, 81 and 63. That is the highest common factor of 45, 81 and 63.

GCF (45, 81, 63)  =  9

9 is the greatest number of plants Jill can put in one row. 

Answer (3) :

Because the two numbers are in the ratio 6 : 7, the numbers are assumed to be 6x and 7x.

GCF (6x, 7x)  =  x

But, it is given that GCF of two numbers is 13.

Then, 

x  =  13

Substitute 13 for x in 6x and 7x. 

6(13)  =  78

7(13)  =  91

The two numbers are 78 and 91.

Answer (4) : 

For example, let the large and small gears complete a rotation every 3 seconds and 4 seconds respectively. 

Then the large gear completed rotations in 3, 6, 9, 12 seconds... 

Like this, the small gear completes rotations in 4, 8, 12 seconds... 

So, if the two gears are aligned now, again they will align in 12 seconds. This 12 seconds is the least common multiple (LCM) of 3 and 4. 

The same thing happened in our problem. To find the time pass before the gears align again, we have to find the least common multiple of 45 seconds and 18 seconds. 

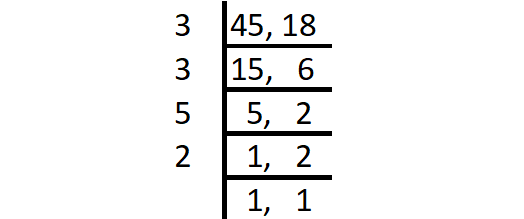
LCM (45, 18)  =  Product of all prime factors

=  3 ⋅ 3 ⋅ 5 ⋅ 2

=  90

90 seconds will pass before the gears are aligned again. 

Answer (5) : 

To find the least number of rose bushes, we have to find the least number that is evenly divisible by 12 and 15. That is the least common multiple of 12 and 15.

Find the least common multiple of 12 and 15.

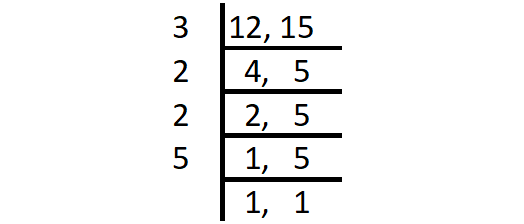
LCM (12, 15)  =  Product of all prime factors

=  3 ⋅ 2 ⋅ 2 ⋅ 5

=  60

60 is the least number of rose bushes Dante could have.

Answer (6) : 

Because the two numbers are in the ratio 5 : 7, the numbers are assumed to be 5x and 9x.

But, it is given that the second number is 72.

Then, 

9x  =  72

Divide each side by 9.

x  =  8

The first number  =  5(8)  =  40.   

Find the least common multiple of 40 and 72.

LCM (40, 72)  =  Product of all prime factors

=  2 ⋅ 2 ⋅ 2 ⋅ 5 ⋅ 3 ⋅ 3

=  360

The least common multiple of the two numbers is 360.

Apart from the stuff given in this section,  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.