GCD OF ALGEBRAIC EXPRESSIONS

Example :

Find the GCD of the following

(i)  c²-d², c(c-d)

(ii)  x⁴-27a³x, (x-3a)²

(iii)  m²-3m-18,  m²+5m+6

(iv)  x²+14x+33, x³+10x²-11x

(v)  x²+3xy+2y², x²+5xy+6y²

(vi)  2x²-x-1, 4x²+8x+3

(vii)  x²-x-2, x²+x-6, 3x²-13x+14

(viii)  x³-x²+x-1, x⁴ - 1

(ix)  24 (6x⁴-x³-2x²), 20(2x⁶+3x⁵+x⁴)

(x)  (a-1)⁵ (a+3)², (a-2)² (a-1)³ (a+3)⁴

(i)  Answer :

c²-d², c(c-d)

By using algebraic identity

a²-b²  =  (a+b)(a-b)

c²-d²=  (c+d) (c-d) 

c(c - d)  =  c(c - d)

Common factor is (c-d).

So, greatest common divisor is (c - d).

(ii)  Answer :

x⁴-27a³x, (x-3a)² 

x⁴-27a³x  =  x(x³-27a³)

=  x(x³-(3a)³)

By using algebraic identity

a³-b³  =  (a-b)(a²+ab+b²)

x³-(3a)³  =  (x-3a)(x²+3ax+9a²)

x(x³-(3a)³)  =  x(x-3a)(x²+3ax+9a²) ----(1)

(x-3a)²  =  (x-3a)(x-3a) ----(2)

Common factors of (1) and (2) are (x-3a).

So, greatest common divisor is (x-3a).

(iii)  Answer :

m²-3m-18,  m²+5m+6

By doing factorization, we get

m²-3m-18  =  (m-6) (m+3)

m²+5m+6  =  (m+2) (m+3)

Common factor is (m+3).

So, greatest common divisor is (m+3).

(iv)  Answer :

x²+14x+33, x³+10x²-11x

x²+14x+33  =  (x+11)(x+3)  ---(1)

x³+10x²-11x  =  x(x²+10x-11)

  =  x(x+11)(x-1)  ----(2)

Common factor is (x+11).

So, greatest common divisor is (x+11).

(v)  Answer :

x²+3xy+2y², x²+5xy+6y²

x²+3xy+2y²  =  x²+xy+2xy+2y²

= x(x+y)+2y(x+y)

=  (x+2y)(x+y)  ---(1)

x²+5xy+6y²  =  x²+2xy+3xy+6y²

=  x(x+2y)+3y(x+2y)

=  (x+2y) (x+3y)----(2)

Greatest common factor of (1) and (2) is (x+2y).

(vi) Answer :

2x²-x-1, 4x²+8x+3

2x²-x-1  =  (2x+1) (x-1)

4x²+8x+3  =  (2x+3)(2x+1)

Common factor is (2x+1). 

So, the greatest common divisor is (2x+1).

(vii) Answer :

x²-x-2, x²+x-6, 3x²-13x+14

x²-x-2  =  (x-2) (x+1)

x²+x-6 =  (x+3)(x-2)

3x²-13x+14  =  (x-2)(3x-7)

Common factor is (x-2).

So, the greatest common divisor is (x - 2).

(viii)  Answer :

x³-x²+x-1, x⁴ - 1

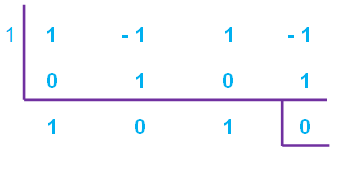
=  (x-1)(x²+1)  ----(1)

x⁴-1  =  (x²)²-(1²)²

=  (x²+1) (x²-1)

=  (x²+1)(x+1)(x-1) ----(2)

Common factors in (1) and (2) are (x-1) and (x²+1)    

So, the greatest common divisor is (x-1)(x²+1).

(ix)  Answer :

24 (6x⁴-x³-2x²), 20(2x⁶+3x⁵+x⁴)

24 (6x⁴-x³-2x²)  =  2³ ⋅ 3 x² (6x²-x-2)

=  2³ ⋅ 3 x² (3x-2) (2x+1)

20(2x⁶+3x⁵+x⁴)  =  5 ⋅ 2² x⁴ (2x²+3x+1)

=  5 ⋅ 2² x⁴ (x+1) (2x+1)

Common factors are 2² x² (2x+1)

So, the greatest common divisor is 4x²(2x + 1).

(x)  Answer :

(a-1)⁵ (a+3)², (a-2)² (a-1)³ (a+3)⁴

The common factors are (a-1)³(a+3)²

So, the greatest common divisor is (a-1)³(a+3)².

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.