FUNDAMENTAL THEOREM OF ARITHMETIC

The fundamental theorem asserts that every composite number can be decomposed as a product of prime numbers and that the decomposition is unique. In the sense that there is one and only way to express the decomposition as product of primes.

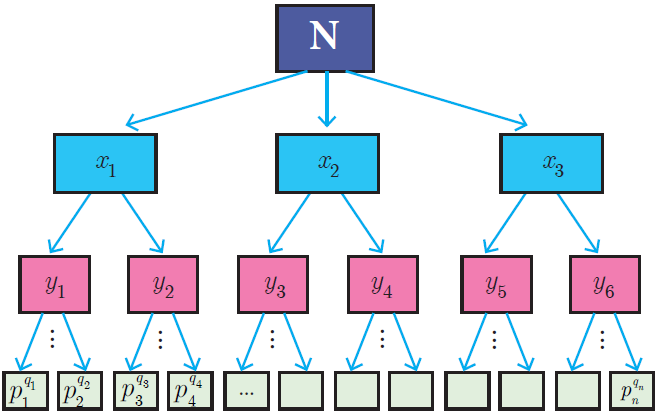
In general, we conclude that given a composite number N, we decompose it uniquely in the form

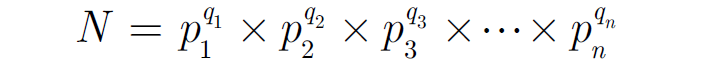
where p₁, p₂, p₃, ...., p_n are primes and q₁, q₂, q₃, ...., q_n are natural numbers.

First, we try to factorize N into its factors. If all the factors are themselves primes then we can stop. Otherwise, we try to further split the factors which are not prime. Continue the process till we get only prime numbers.

Writing the primes in ascending order makes the factorization unique in nature.

Significance of the Fundamental Theorem of Arithmetic

The fundamental theorem about natural numbers except 1, that we have stated above has several applications, both in Mathematics and in other fields. The theorem is vastly important in Mathematics, since it highlights the fact that prime numbers are the ‘Building Blocks’ for all the positive integers. Thus, prime numbers can be compared to atoms making up a molecule

Example 1 : 

In the given factor tree, find the numbers m and n.

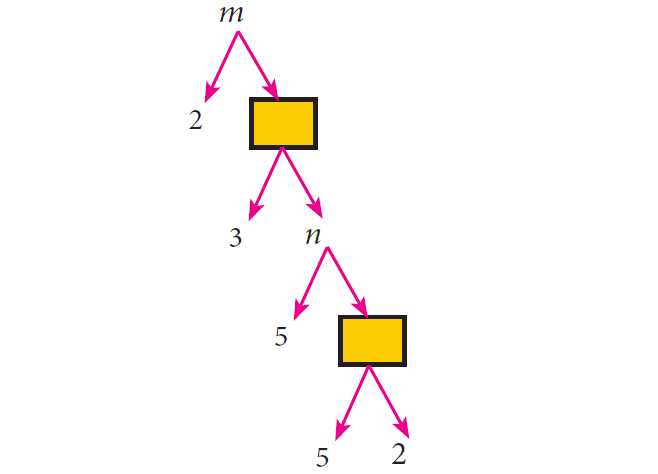
Solution :

Value of the first box from bottom = 5 x 2 = 10.

Value of n = 5 x 10 = 50.

Value of the second box from bottom = 3 x 0 = 150.

Value of m = 2 x 150 = 300.

Thus, the required numbers are m = 300, n = 50. 

Example 2 : 

Can the number 6ⁿ, n being a natural number end with the digit 5? Give reason for your answer.

Solution :

Since 6ⁿ = (2 x 3)n = 2n x 3n, 2 is a factor of 6n . So, 6n is always even.

But any number whose last digit is 5 is always odd.

Hence, 6n cannot end with the digit 5. 

Example 3 : 

Is 7 x 5 x 3 x 2 + 3 a composite number? Justify your answer.

Solution :

Yes, the given number is a composite number, because

7 x 5 x 3 x 2 + 3 = 3(7 x 5 x 2 + 1) = 3 x 71

Since the given number can be factorized in terms of two primes, it is a composite number.

Example 4 : 

a and b are two positive integers such that a^b x b^a = 800. Find a and b.

Solution :

The number 800 can be factorized as

800 = 2 x 2 x 2 x 2 x 2 x 5 x 5 = 2⁵ x 5²

Hence, a^b x b^a = 2⁵ x 5².

This implies that a = 2 and b = 5 (or) a = 5 and b = 2.

Example 4 : 

Explain why (5×7×11+11) and (6 × 5 × 4 × 3 × 2 × 1 + 5) are composite numbers. 

Solution :

= 5 × 7 × 11 + 11

Factoring 11, we get

= 11 (5 × 7 + 1)

=11 × 36

=11 × 2 × 2 × 3 × 3

= 2² × 3² × 11

So, it is composite 

(6 × 5 × 4 × 3 × 2 × 1 + 5)

Factoring 5 out, we get

= 5 x (6 × 4 × 3 × 2 × 1 + 1)

= 5 x (2 x 3 × 2 x 2 × 3 × 2 × 1 + 1)

= 5 x (2⁴ x 3² + 1)

The product of these two numbers will not have only two factors. It will have more factors. Then it is composite.

Example 5 :

If the HCF of two numbers is 1, then the two numbers are called.

a) composite          b) Relative prime or co-prime

c)  Perfect            d) irrational numbers

Solution :

The consecutive numbers which will have highest common factor which is 1. Then the required number is relative prime or coprime.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.