FUNCTIONS WORKSHEET

Problem 1 :

If f(x) = (1/2)x - 1, what is f(-2x + 1) equal to ?

Problem 2 :

If f(x)  = √x + 2 and g(x) = (x - 1)², find g[f(a)] - 2f(a).

Problem 3 :

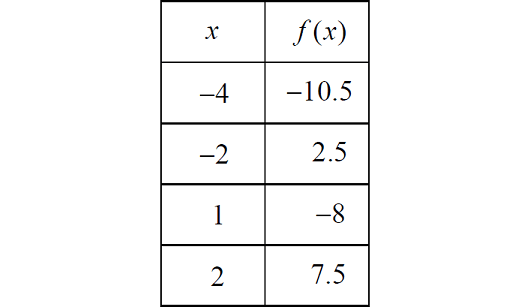
The function f is defined by a polynomial. Some values of x and f(x) are shown in the table above. What is the remainder when f(x) is divided by x + 2?

Problem 4 :

If (x + 2) is a factor f(x) = x³ + x² + x + c and (-1, p) lies on the graph of f, what is the value of p?

Problem 5 :

The table above shows some values of the linear function f. Find f(x).

Problem 6 :

Let the function be f be defined by f(x) = 4x² - 2 and let the function g be defined by g(x) = x³ - 5. Find the value of f[g(1)].

Problem 7 :

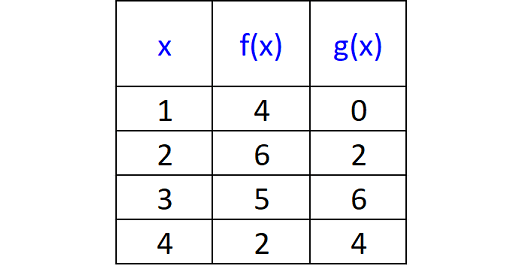
Four values of the functions f and g are shown in the table above. If g(a) = 4, find the value f(a).

Problem 8 :

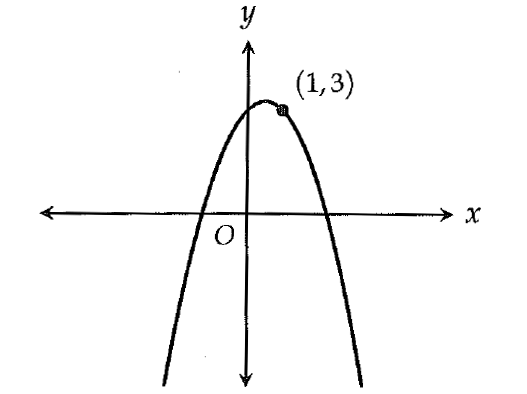
The graph of the function g in the xy-plane is shown above. If f is another function defined in the same xy-plane and f(1) = 1, then g could be which of the following?

A) f - 1

B) f - 2

C) f + 1

D) f + 2

Problem 9 :

f(x) = ax³ + b

In the function f defined above, 'a' and 'b' are constants. If f(-1) = 4 and f(1) = 10, find the value of 'b'.

Problem 10 :

The function f is graphed in the xy-plane shown below.

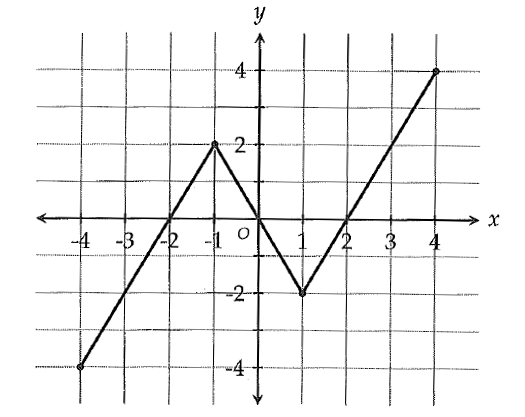
If f(c) = f(3), which of the following could be the value of 'c'?

A) -3

B) -2

C) -1

D) 2

Answers

1. Answer :

f(x) = (1/2)x - 1

Replace 'x' by '-2x + 1'.

f(-2x + 1) = (1/2)(-2x + 1) - 1

= (1/2)(-2x) + (1/2)(1) - 1

= -x + 1/2 - 1

= -x - 1/2

2. Answer :

f(x) = √x + 2 and g(x) = (x - 1)²

f(a) = √a + 2

g[f(a)] - 2f(a) = g[√a + 2] - 2(√a + 2)

= (√a + 2 - 1)² - 2√a - 4

= (√a + 1)² - 2√a - 4

= (√a + 1)(√a + 1) - 2√a - 4

= (√a)² + √a + √a + 1 - 2√a - 4

= (√a)² + 2√a + 1 - 2√a - 4

= a - 3

3. Answer :

Equate the divisor (x + 2) to zero and solve for x.

x + 2 = 0

x = -2

Now, substitute x = -2 in f(x) to get the remainder when f(x) is divided by x + 2.

Remainder = f(-2)

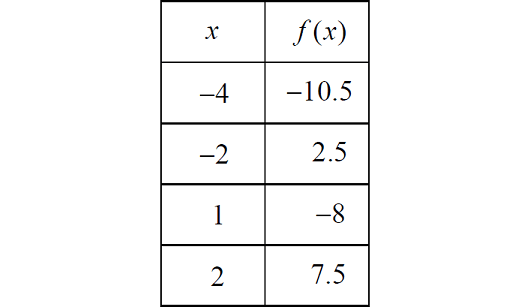
In the table above, when x = -2, f(x) = 2.5.

Remainder = 2.5

4. Answer :

Equate the factor (x + 2) to zero and solve for x.

x + 2 = 0

x = -2

When you substitute x = -2 in f(x), it will become zero. Because (x + 2) is a factor of f(x).

f(-2) = 0

(-2)³ + (-2)² + (-2) + c = 0

-8 + 4 - 2 + c = 0

-6 + c = 0

c = 6

f(x) = x³ + x² + x + 6

The point (-1, p) lies on the graph of f. 

So, substitute x = -1 and f(x) = p in f(x) = x³ + x² + x + 6.

p = (-1)³ + (-1)² + (-1) + 6

= -1 + 1 - 1 + 6

= 5

5. Answer :

Choose any two points from the table above to find the slope.

(-1, 9) and (1, 3)

Slope of a line = (y₂ - y₁)/(x₂ - x₁)

Substitute (x₁, y₁) = (-1, 9) and (x₂, y₂) = (1, 3).

Slope of a line = (3 - 9)/(1 + 1)

= -6/2

= -3

Equation of line in slope intercept-form :

y = -3x + b

We can use one of the points from the table to find y-intercept 'b'.

Substitute (1, 3) in y = -3x + b.

3 = -3(1) + b

3 = -3 + b

6 = b

Therefore, 

y = -3x + 6

or

f(x) = -3x + 6

6. Answer :

g(1) = 1³ - 5

= 1 - 5

= -4

f[g(1)] = f(-4)

= 4(-4)² - 2

= 4(16) - 2

= 64 - 2

= 62

7. Answer :

g(a) = 4 ----(1)

In the table above, when x = 4, g(x) = 4.

So,

g(4) = 4 ----(2)

Comparing (1) and (2),

a = 4

f(m) = f(4)

In the table above, when x = 4, f(x) = 2.

Therefore,

f(m) = 2

8. Answer :

Given : f(1) = 1.

So, the point (1, 1) is on the graph of the function f. 

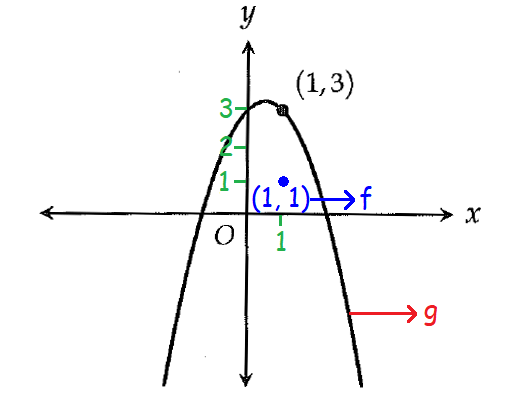
From the picture above, to get the graph of the function g, we have to do a vertical translation of the graph of f by 2 units up.

Thus,

g = f + 2

The correct answer choice is option (D) f + 2.

9. Answer :

f(x) = ax³ + b

f(-1) = 4

a(-1)³ + b = 4

a(-1) + b = 4

-a + b = 4 ----(1)

f(1) = 10

a(1)³ + b = 10

a + b = 4 ----(2)

(1) + (2) :

2b = 14

Divide both sides by 2.

b = 7

10. Answer :

In the graph above, when x = 3, f(x) = 2.

That is,

f(3) = 2

It is given that

f(c) = f(3).

Substitute 2 for f(3).

f(c) = 2.

In the graph above, f(x) = 2 when x = -1 or x = 3.

Therefore, c = -1 or 3.

In the given options, we have -1 only.

The correct answer choice is (C) -1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.