FUNCTION NOTATION INPUT AND OUTPUT

Function notation is the other way of writing an equation which can be used to represent the total amount.

In a function, you can plug in an input value, some operations are performed on the input value, then out put value is produced.

For example, if you can pump 25 cubic feet of water per minute into a tank, you can use v to represent the volume of water in the tank and t to represent the amount of time the tank is being filled. You can that the volume of water in the tank is a function of time. Because the volume of water v in the tank is depending only on the amount time t that has passed.

Instead of just using v to represent the volume, the notation v(t) can be used to show that v is a function of time t.

v(t) ----> pronounced v of t

Therefore, the function representing the relationship between v and t in the example above is written as

v(t) = 25t

In the function above, if t = 1,

v(1) = 25(1) = 25 ft.³

That is, in 1 minute, the tank is filled with 25 cubic feet of water.

If t = 2,

v(2) = 25(2) = 50 ft.³

In 2 minutes, the tank is filled with 50 cubic feet of water.

Let someone start pumping water into the tank now. How much water will be in the tank after 30 minutes?

To find the amount of water in the tank after 30 minutes, we have plug in 30 for t into the function v(t).

v(30) = 25(30)

= 750 ft.³

Note :

v(t) does not mean v times t. v(t) represents the value of v for the given value of t.

For example, v(3) represents the value of v, when t = 3.

Example 1 :

Let f(x) = 3x + 2. Find the values of the following.

(i) f(1)

(ii) f(-2)

(iii) f(⁻¹⁄₃)

(iv) f(½)

Solution :

(i) f(1) :

f(x) = 3x + 2

f(1) = 3(1) + 2

= 3 + 2

= 5

(iii) f(⁻¹⁄₃) :

f(x) = 3x + 2

f(⁻¹⁄₃) = 3(⁻¹⁄₃) + 2

= -1 + 2

= 1

(ii) f(-2) :

f(x) = 3x + 2

f(1) = 3(-2) + 2

= -6 + 2

= -4

(iv) f(½) :

f(x) = 3x + 2

f(½) = 3(½) + 2

= ³⁄₂ + 2

= ³⁄₂ + ⁴⁄₂

= ⁽³ ⁺ ⁴⁾⁄₂

= ⁷⁄₂

Example 2 :

Let g(x) = -2x + 5.

Find the values of the following.

(i) g(-1)

(ii) g(3)

(iii) g(⁻¹⁄₂)

(iv) g(¼)

Solution :

(i) g(-1) :

g(x) = -2x + 5

g(-1) = -2(-1) + 5

= 2 + 5

= 7

(iii) g(⁻¹⁄₂) :

g(x) = -2x + 5

g(⁻¹⁄₂) = -2(⁻¹⁄₂) + 5

= -1 + 5

= 4

(ii) g(3) :

g(x) = -2x + 5

g(3) = -2(3) + 5

= -6 + 5

= 11

(iv) g(¼) :

g(x) = -2x + 5

g(¹⁄4) = -2(¹⁄4) + 5

= ⁻¹⁄₂ + 5

= ⁻¹⁄₂ + ²⁄₂

= ⁽⁻¹ ⁺ ²⁾⁄₂

= ¹⁄₂

Example 3 :

Let h(x) = (½)x + 5.

Find the values of the following.

(i) h(-2)

(ii) h(0)

(iii) h(4)

(iv) h(1)

Solution :

(i) h(-2) :

h(x) = (½)x + 5

h(-2) = (½)(-2) + 5

= -1 + 5

= 4

(iii) h(4) :

h(x) = (½)x + 5

h(4) = (½)(4) + 5

= 2 + 5

= 7

(ii) h(0) :

h(x) = (½)x + 5

h(0) = (½)(0) + 5

= 0 + 5

= 5

(iv) h(1) :

h(x) = (½)x + 5

h(1) = (½)(1) + 5

= ½ + 5

= ½ + ¹⁰⁄₂

= ⁽¹ ⁺ ¹⁰⁾⁄₂

= ¹¹⁄₂

Example 4 :

Let f(x) = 2x - 1.

Find the value of x for the given value of f(x).

(i) f(x) = 13

(ii) f(x) = -3

(iii) f(x) = 0

(iv) f(x) = ½

Solution :

(i) f(x) = 13 :

f(x) = 13

2x - 1 = 13

2x = 14

x = 7

(iii) f(x) = 0 :

f(x) = 0

2x - 1 = 0

2x = 1

x = ½

(ii) f(x) = -3 :

f(x) = -3

2x - 1 = -3

2x = -2

x = -1

(iv) f(x) = ½ :

f(x) = ½

2x - 1 = ½

2x = ½ + 1

2x= ½ + ¹⁰⁄₂

2x = ⁽¹ ⁺ ¹⁰⁾⁄₂

2x = ¹¹⁄₂

x = ¹¹⁄4

Example 5 :

Let g(x) = -3x + 4.

Find the value of x for the given value of f(x).

(i) g(x) = 1

(ii) g(x) = -5

(iii) g(x) = 0

(iv) g(x) = ½

Solution :

(i) g(x) = 1 :

g(x) = 1

-3x + 4 = 1

-3x = -3

x = 1

(iii) g(x) = 0 :

g(x) = 0

-3x + 4 = 0

-3x = 4

x = ⁻⁴⁄₃

(ii) g(x) = -3

g(x) = -5

-3x + 4 = -5

-3x = -9

x = 3

(iv) g(x) = ½ :

f(x) = ½

-3x + 4 = ½

-3x = ½ - 4

-3x= ½ - ⁸⁄₂

-3x = ⁽¹ ⁻ ⁸⁾⁄₂

-3x = ⁻⁷⁄₂

3x = ⁷⁄₂

x = ⁷⁄₆

Example 6 :

Let h(x) = (⁻²⁄₃)x + 5.

Find the value x for the given value of h(x).

(i) h(x) = 7

(ii) h(x) = 0

(iii) h(x) = -1

(iv) h(x) = ⁻¹⁄₂

Solution :

(i) h(x) = 7 :

h(x) = 7

(⁻²⁄₃)x + 5 = 7

(⁻²⁄₃)x = 2

-2x = 6

x = -3

(iii) h(x) = -1 :

h(x) = -1

(⁻²⁄₃)x + 5 = -1

(⁻²⁄₃)x = -6

-2x = -18

2x = 18

x = 9

(ii) h(x) = 0

h(x) = 0

(⁻²⁄₃)x + 5 = 0

(⁻²⁄₃)x = -5

-2x = -15

2x = 15

x = ¹⁵⁄₂

(iv) h(x) = ⁻¹⁄₂ :

h(x) = ⁻¹⁄₂

(⁻²⁄₃)x + 5 = ⁻¹⁄₂

(⁻²⁄₃)x = ⁻¹⁄₂ - 5

(⁻²⁄₃)x = ⁻¹⁄₂ - ¹⁰⁄₂

(⁻²⁄₃)x = ⁽⁻¹ ⁻ ¹⁰⁾⁄₂

(⁻²⁄₃)x = ⁻¹¹⁄₂

(²⁄₃)x = ¹¹⁄₂

2x = ³³⁄₂

x = ³³⁄4

Example 7 :

f(x) = 3x + b

In the function above, b is a constant. If f(2) = 8, find the value of f(-1).

Solution :

To find the value of f(-1), first we have to find the value of the constant b in f(x) = 3x + b.

Given : f(x) = 3x + b and f(2) = 8.

f(x) = 3x + b

f(2) = 3(2) + b

f(2) = 6 + b ----(1)

f(2) = 8 ----(2)

From (1) and (2),

6 + b = 8

b = 2

Now, the given function is

f(x) = 3x + 2

Substitute x = -1.

f(-1) = 3(-1) + 2

= -3 + 2

= -1

Example 8 :

Let f(x + 3) = -7x + 5. Find the value of f(2).

Solution :

The given function is not in the form f(x). So, we can not substitute x = 2 in f(x + 3). First, we have to change the given function to the regular form f(y). Then, we have to substitute y = 2 to evaluate f(2).

f(x + 3) = -7x + 5 ----(1)

Let y = x + 3.

Solve for x in terms of y.

y = x + 3

y - 3 = x

Substitute y for 'x + 3' and 'y - 3' for x in (1).

f(y) = -7(y - 3) + 5

f(y) = -7y + 21 + 5

f(y) = -7y + 26

Substitute y = 2.

f(2) = -7(2) + 26

f(2) = -14 + 26

f(2) = 12

Example 9 :

A house security company is charging house owner a onetime setup fee $175 plus y dollars for each month of monitoring the house. Find the function which models the total charge for 12 months. And also, find the total charge, if the monthly charge is $15.

Solution :

It is given that the monthly charge is y dollars.

1 month ----> $y

12(1 month) ----> 12($y)

12 months = 12y

Total charge for 12 months (including onetime setup fee) :

= 12y + 175

Therefore, the function which models the total charge for 12 months :

T(y) = 12y + 175

To find the total charge, when the monthly charge is $15, substitute y = 15 into the above function.

T(15) = 12(15) + 175

= 180 + 175

= 355

If the monthly charge is $15, then the total charge for 12 months is $355.

Example 10 :

A taxi service charges a flat rate of $20 plus $3.25 for each mile travelled. Write a function which represents the total charge for x number of miles travelled. And also, find the total charge for 40 miles travelled.

Solution :

It is given that the charge for each mile travelled is $3.25.

1 mile ----> $3.25

x(1 mile) ----> x($3.25)

x miles ----> $3.25x

Total charge for x miles (including the flat rate) :

= 3.25x + 20

Therefore, the function which models the total charge for x miles :

f(x) = 3.25x + 20

To find the total charge for 40 miles travelled, substitute x = 40 into the above function.

f(40) = 3.25(40) + 20

= 130 + 20

= 150

The total charge for 40 miles travelled is $150.

Practice Questions

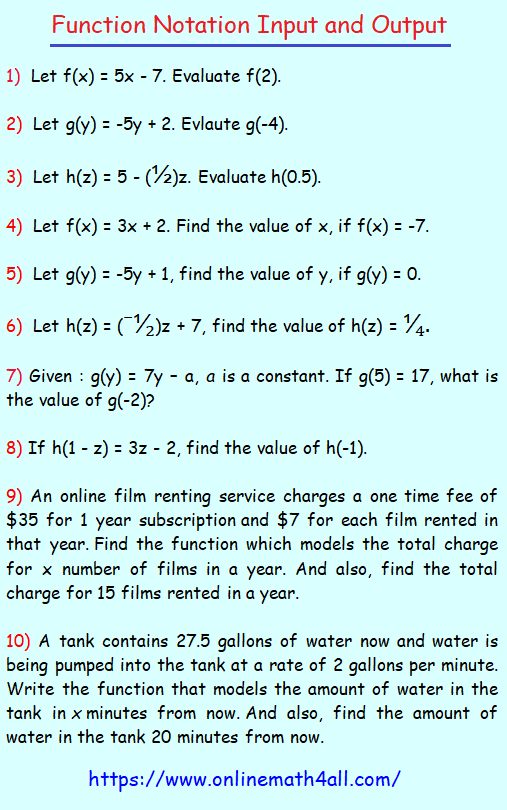
Click here to get detailed answers for the above questions.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

FUNCTION NOTATION INPUT AND OUTPUT

Practice Questions

Recent Articles

De Moivre's Theorem and Its Applications

First Fundamental Theorem of Calculus - Part 1

Polar Form of a Complex Number