FUNCTION NOTATION AND EVALUATION

Function notation is the way in which a function can be represented. It is the simple way of giving information about the function.

The notation y = f(x) provides a way of denoting the value of y (the dependent variable) that corresponds to some input value x (the independent variable).

The most popular and widely used function notation is f(x) which has to be read as 'f' of 'x'. 

Here f and x are NOT multiplied.

Always functions are referred to by single letter names, like f, g, h and so on. Any letter can be used to name a function. 

Let us consider the brightness of an electric bulb.

Let f stand for the brightness of the bulb and x stand for the voltage of electricity given to the bulb.

Here f depends on x. 

More clearly, the output of f (brightness) is depending on x (voltage).

So it will be written as f(x). When we plug some value for x (input), accordingly we will get some value for "f" (output).

It has been illustrated in the given figure.  

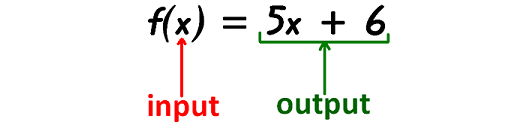
Let us look at some more examples. 

f(x) = 3x² + 5, g(x) = 3x - 7,  h(x) = ax² + bx + c, s(t) = 1/t

Instead of f(x), sometimes we will be representing a function by y.

That is,  y = f(x).

Then the function f(x) = 5x + 6 will become y = 5x + 6.

Here, the value of x is input and the value of y is out put. 

The equation of a graph is mostly represented as y = f(x) and in the ordered pair (x, y), x stands for the value on x- axis and y stands for the value on y-axis.  

Note :

The notation f : X ----> Y tells us that f is the rule which are mapping the elements from the set X to set Y.

The arrow has to be read as "mapped to".

Applications of Function Notation

1. Since different functions are represented using different variables like f, g, h, it avoids confusion as to which function is being examined.

2. It allows us to quickly identify the independent variable.

For example, in the function f(x) = ax² + bx + c, the independent variable is x.

3. It allows to quickly state which element of the function has to be examined.

For example, in the function f(x) = 4x + 5, if the question says "find f(3)", we can understand that we have to find the value of "y" when x = 3.

Evaluating Functions

Example 1 : 

Evaluate f(4) where f(x) = 3(2x + 1).

Solution :

f(x) = 3(2x + 1)

Substitute x = 4. 

f(4) = 3[2(4) + 1]

= 3[8 + 1]

= 3(9)

= 27

Example 2 : 

Evaluate f(w + 2) where f(x) = x² + 3x + 5.

Solution :

f(x) = x² + 3x + 5

Substitute x = w + 2.

f(w + 2) = (w + 2)² + 3(w + 2) + 5

= (w + 2)(w + 2) + 3w + 6 + 5

= w² + 2w + 2w + 4 + 3w + 6 + 5

= w² + 7w + 15

Example 3 :

Given f(x) = x² - x - 4, if f(k) = 8, what is the value of k?

Solution :

f(k) = 8

k² - k - 4 = 8

Subtract 8 from both sides.

k² - k - 12 = 0

factor and solve.

(k + 3)(x - 4) = 0

k + 3 = 0   or   k - 4 = 0

k = -3   or   k = 4

Example 4 :

The number of pounds p of carbon dioxide produced by a car is 20 times the number of gallons g of gasoline used by the car. Write and graph a function that describes the relationship between g and p.

Solution :

p - number of pounds of carbon dioxide produced by the car

g - number of gallons of gasoline used by the car.

p = 20g

• When g = 1, p = 20(1) ==> 20
• When g = 2, p = 20(2) ==> 40
• When g = 3, p = 20(3) ==> 60

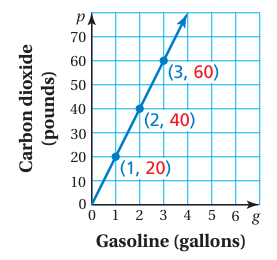
Plot the ordered pairs and draw a line through the points. Because you cannot have a negative number of gallons, use only positive values of g.

Example 5 :

You decide to make and sell bracelets. The cost of your materials is $84. You charge $3.50 for each bracelet.

a. Write a function that represents the profit P for selling b bracelets.

b. Which variable is independent? dependent? Explain.

c. You will break even when the cost of your materials equals your income. How many bracelets must you sell to break even?

Solution :

Cost of material = $84

Cost per bracelet = $3.50

a) Profit = Selling price - Cost price

Number of bracelets selling is b

Selling price of each bracelet = $3.50

Selling price of b bracelets = 3.50b

profit = 84 - 3.50b

b) 

• b (number of bracelets selling is the independent variable)
• p(profit) is the dependent variable.

c) At break even point, cost price and selling price will be equal.

84 = 3.5b

b = 84/3.5

b = 24

While selling 24 bracelets there is no loss and no profit.

Example 6 :

A furniture store is having a sale where everything is 40% off.

a. Write a function that represents the amount of discount d on an item with a regular price p.

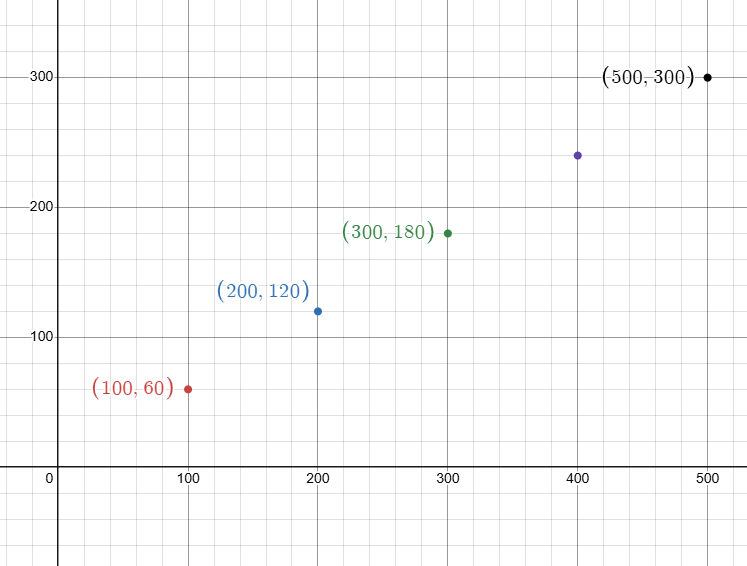
b. Graph the function using the inputs 100, 200, 300, 400, and 500 for p.

c. You buy a bookshelf that has a regular price of $85. What is the sale price of the bookshelf?

Solution :

Regular price = p

Since the discount is 40%, then the amount we pay is 60% of the original price.

a)

d = 60% of p

= 0.6p

b) 

c)

Regular price = 85

discounted price = 0.6(85)

= 51

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.