FRACTIONS DECIMALS AND PERCENTAGES

Fraction, decimal and percentages are all just different ways of showing the same value. 

It has been clearly explained here.

A half can be written as follows

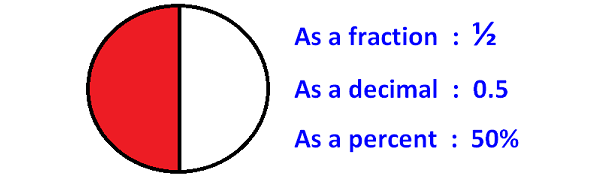
A quarter can be written as follows

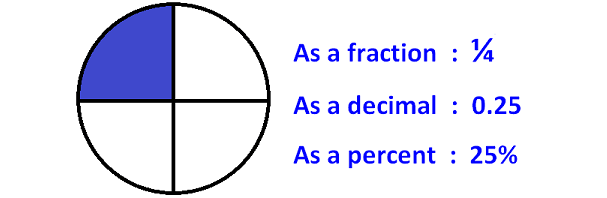
Conversions

Proper Fraction to Decimal

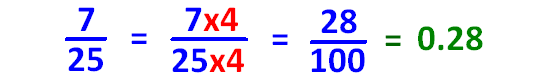
Improper Fraction to Decimal

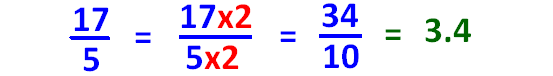
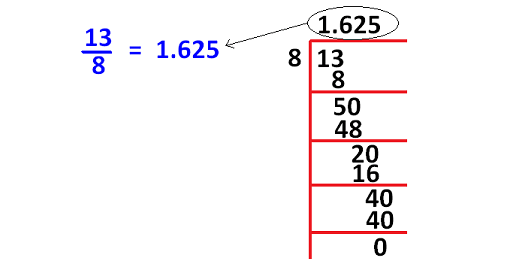
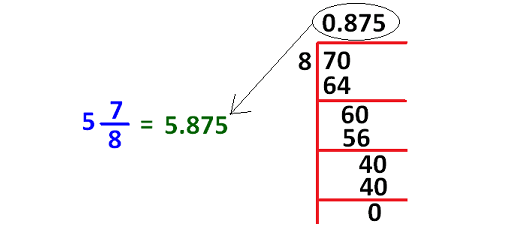
Mixed Fraction to Decimal

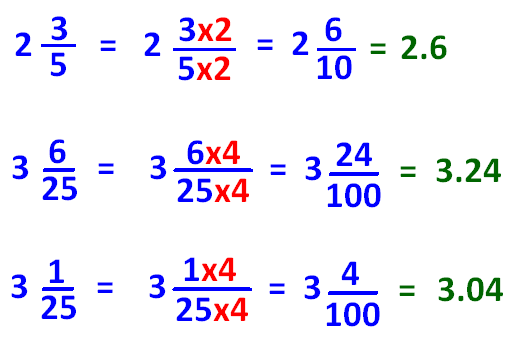
Proper Fraction to Percentage

Improper Fraction to Percentage

Decimal to Percentage

Decimal to Fraction

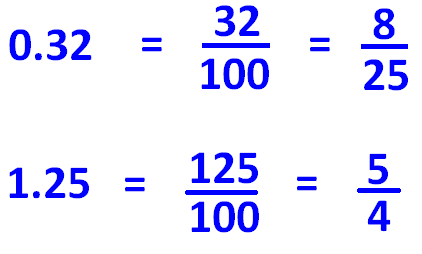
Percentage to Fraction

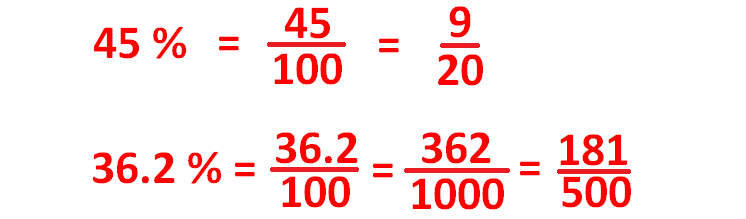
Percentage to Decimal

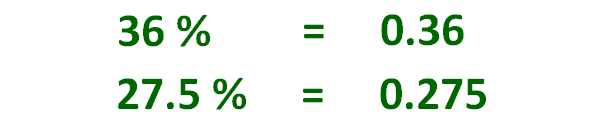
Solved Problems

Problem 1 :

Convert the given fraction to decimal

⁹⁄₂₅

Solution :

In the given fraction, the denominator is 20 which is convertible to 100 using multiplication by 4.

Then, we have

Problem 2 :

Covert the given fraction to decimal

⅖

Solution :

In the given fraction, the denominator is 5 which is convertible to 10 using multiplication by 2.

Then, we have

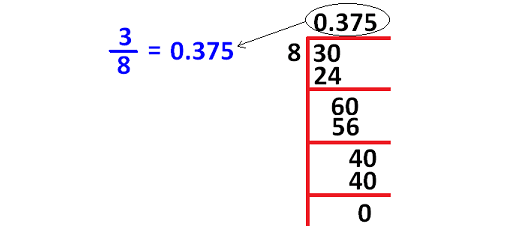
Problem 3 :

Covert the fraction to decimal

⅞

Solution :

In the fraction number, the denominator is 8 which is convertible to 1000 using multiplication by 125. 

Problem 4 :

Covert the fraction to percentage.

¾

Solution :

To convert any fraction to percentage, we have to make the denominator as 100 using multiplication.

In the fraction ¾, the denominator is 4 which is convertible to 100 using multiplication by 4.

Problem 5 : 

Convert the given fraction to percentage.

¹⁰⁄₃

Solution :

In the fraction ¹⁰⁄₃, the denominator is 3 which can not be converted to 100 using multiplication. 

So the given fraction can be converted to decimal using long division.  

Then, we have

¹⁰⁄₃  ≈  3.3333  (approximately)

Multiply 3.3333 by 100 to convert it to percent.

3.3333 ⋅ 100% ≈ 333.33%

Problem 6 :

Covert the decimal to fraction.

0.23

Solution :

To convert any decimal into fraction, first get rid of the decimal point using multiplication of 10, 100, 1000...... and so on.

You can write 0.23 as a fraction with denominator 1.

0.23 = ⁰^.²³⁄₁

In 0.23, there are two digits after the decimal. So, multiply both numerator and denominator by 100.

Problem 7 :

Covert the decimal to fraction.

0.004

Solution :

To convert any decimal into fraction, first get rid of the decimal point using multiplication of 10, 100, 1000...... and so on.

In 0.004, there are three digits after the decimal.

You can write 0.004 as a fraction with denominator 1.

0.004 = ⁰^.⁰⁰⁴⁄₁

In 0.004, there are three digits after the decimal. So, multiply both numerator and denominator by 1000.

Problem 8 :

Covert the decimal to percentage.

0.32

Solution :

To convert 0.32 to percentage, multiply it by 100.

0.32 = 0.32 x 100%

0.32 = 32%

Problem 9 :

Covert the decimal to percentage.

0.005

Solution :

To convert 0.005 to percentage, multiply it by 100.

0.005 = 0.005 x 100%

0.005 = 0.5%

Problem 10 :

Covert the percentage to fraction.

64%

Solution :

Percentage is comparing the value to 100. 

Then, we have

64% = ⁶⁴⁄₁₀₀

64% = ¹⁶⁄₂₅

Problem 11 :

Covert the percentage to fraction.

0.8%

Solution :

0.8% = ⁰^.⁸⁄₁₀₀

In 0.8, we have one digit after the decimal point. To get rid of the decimal point in 0.8, multiply both numerator and denominator by 10.

Problem 12 :

Covert the percentage to decimal.

50%

Solution :

Percentage is comparing the value to 100. 

Then, we have

50% = ⁵⁰⁄₁₀₀

50% =  0.50

50% =  0.5

Problem 13 :

Covert the percentage to decimal.

0.06%

Solution :

Percentage is comparing the value to 100. 

Then, we have

0.06% = ⁰^.⁰⁶⁄₁₀₀

0.06% = 0.0006

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.