FORMATION OF QUADRATIC EQUATION WITH GIVEN ROOTS

If α and β are the two roots of a quadratic equation, then the formula to construct the quadratic equation is 

x² - (α + β)x + αβ = 0

That is,

x² - (sum of roots)x + product of roots = 0

If a quadratic equation is given in standard form, we can find the sum and product of the roots using coefficient of x², x and constant term.

Let us consider the standard form of a quadratic equation,

ax² + bx + c = 0

(a, b and c are real and rational numbers)

Let α and β be the two zeros of the above quadratic equation.

Then the formula to get sum and product of the roots of a quadratic equation :

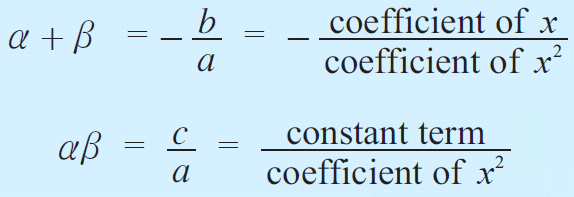
Note :

Irrational roots of a quadratic equation occur in conjugate pairs.

That is, if (m + √n) is a root, then  (m - √n) is the other root of the same quadratic equation equation.

Example 1 :

Form the quadratic equation whose roots are 2 and 3.

Solution :

Sum of the roots is

= 2 + 3

= 5

Product of the roots is

= 2 x 3

= 6

Formation of quadratic equation :

x² - (sum of the roots)x + product of the roots = 0

x² - 5x + 6 = 0

Example 2 :

Form the quadratic equation whose roots are 1/4 and -1.

Solution :

Sum of the roots is

= 1/4 + (-1)

= 1/4 - 1

= 1/4 - 4/4

= (1 - 4)/4

= -3/4

Product of the roots is

= (1/4) x (-1)

= -1/4

Formation of quadratic equation :

x² - (sum of the roots)x + product of the roots = 0

x² - (-3/4)x + (-1/4) = 0

x² + (3/4)x - 1/4 = 0

Multiply each side by 4.

4x² + 3x - 1 = 0

Example 3 :

Form the quadratic equation whose roots are 2/3 and 5/2.

Solution :

Sum of the roots is

= 2/3 + 5/2

The least common multiplication of the denominators 3 and 2 is 6.

Make each denominator as 6 using multiplication.

Then,

= 4/6 + 15/6

= (4 + 15)/6

= 19/6  

Product of the roots is

= 2/3 x 5/2

= 5/3

Formation of quadratic equation :

x² - (sum of the roots)x + product of the roots = 0

x² - (19/6)x + 5/3 = 0

Multiply each side by 6.

6x² - 19x + 10 = 0

Example 4 :

If one root of a quadratic equation (2 + √3), then form the equation given that the roots are irrational.

Solution :

(2 + √3) is an irrational number.

We already know the fact that irrational roots of a quadratic equation will occur in conjugate pairs.

That is,  if (2 + √3) is one root of a quadratic equation, then (2 - √3) will be the other root of the same equation.

So, (2 + √3) and (2 - √3) are the roots of the required quadratic equation.

Sum of the roots is

= (2 + √3) + (2 - √3)

= 4

Product of the roots is

= (2 + √3)(2 - √3)

= 2² - √3²

= 4 - 3

= 1

Formation of quadratic equation :

x² - (sum of the roots)x + product of the roots = 0

x² - 4x + 1 = 0

Example 5 :

If α and β be the roots of x² + 7x + 12 = 0, find the quadratic equation whose roots are

(α + β)² and (α - β)²

Solution :

Given : α and β be the roots of x² + 7x + 12 = 0.

Then,

sum of roots = -coefficient of x/coefficient of x²

α + β = -7/1

= -7

product of roots = constant term/coefficient of x²

αβ = 12/1

= 12

Quadratic equation with roots (α + β)² and (α - β)² is

x² - [(α + β)² + (α - β)²]x + (α + β)²(α - β)² = 0 ----(1)

Find the values of (α + β)² and (α - β)².

(α + β)² = (-7)²

(α + β)² = 49

(α - β)² = (α + β)² - 4αβ

(α - β)² = (-7)² - 4(12)

(α - β)² = 49 - 48

(α - β)² = 1

So, the required quadratic equation is

(1)----> x² - [49 + 1]x + 49 ⋅ 1 = 0

x² - 50x + 49 = 0

Example 6 :

If α and β be the roots of x² + px + q = 0, find the quadratic equation whose roots are

α/β and β/α

Solution :

Given : α and β be the roots of x² + px + q = 0.

Then,

sum of roots = -coefficient of x/coefficient of x²

α + β = -p/1

α + β = -p

product of roots  =  constant term/coefficient of x²

αβ = q/1

αβ = q

Quadratic equation with roots α/β and β/α is

x² - (α/β + β/α)x + (α/β)(β/α) = 0

x² - [α/β + β/α]x + 1 = 0 ----(1)

Find the value of (α/β + β/α).

α/β + β/α = α²/αβ + β²/αβ

= (α² + β²)/αβ

= [(α + β)² - 2αβ]/αβ

= (p² - 2q)/q

So, the required quadratic equation is

(1)----> x² -[(p² - 2q)/q]x + 1 = 0

Multiply each side by q.

qx² - (p² - 2q)x + q = 0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.