FIRST DERIVATIVE TEST FOR RELATIVE MAXIMUM AND MINIMUM

Relative Maximum :

A relative maximum point is a point where the function changes direction from increasing to decreasing (making that point a "peak" in the graph).

Relative Minimum :

Similarly, a relative minimum point is a point where the function changes direction from decreasing to increasing (making that point a "bottom" in the graph).

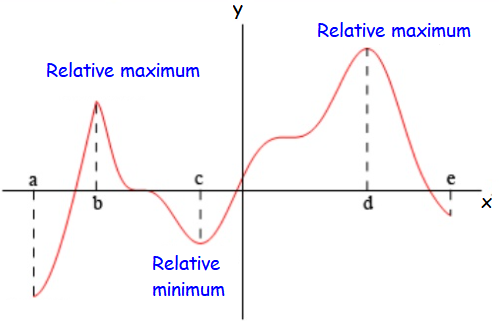
If the first derivative is negative to the left of the critical point and positive to the right of critical point, it has relative minimum at c.

If the first derivative is positive to the left of the critical point and negative to the right of critical point, it has relative maximum at c.

Example 1 :

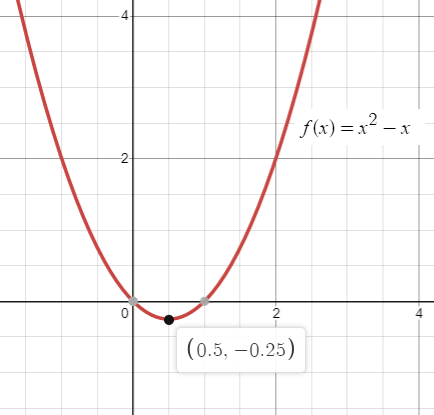
The function defined by f(x)  =  x² - x for all real values of x has relative maximum and relative minimum at x = ?.

Solution :

f(x)  =  x² - x

f'(x)  =  2x-1

f'(x)  =  0

2x-1  =  0

x  =  1/2

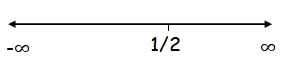
To the left of the critical point :

Let x = 0 ∈ (- ∞, 1/2)

f'(x)  =  2x-1

f'(0)  =  -1 < 0 (Negative)

To the right of the critical point :

Let x = 1 ∈ (1/2, ∞)

f'(1)  =  1 > 0 (Positive)

Result :

The curve is changing its direction from decreasing to increasing. So, there is relative minimum at x  =  c.

Relative minimum at x  =  1/2.

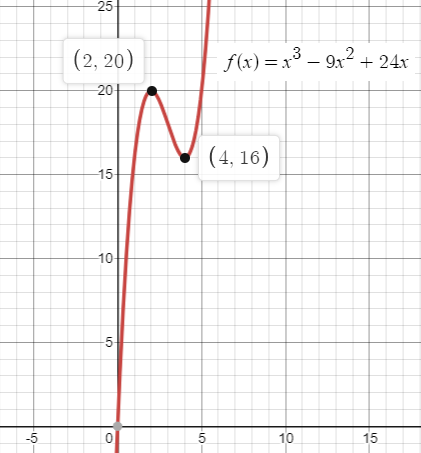
Example 2 :

The function defined by

f(x)  =  x³-9x²+24x

for all real values of x has relative maximum and relative minimum at x = ?.

Solution :

f(x)  =  x³-9x²+24x

f'(x)  =  3x²-18x+24

f'(x)  =  0

3x²-18x+24  =  0

x²-6x+8  =  0

(x-2)(x-4)  =  0

x  =  2 and x  =  4

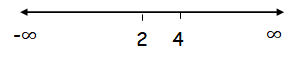
To the left of the critical point at x  =  2 :

Let x = 0 ∈ (- ∞, 2)

f'(x)  =  (x-2)(x-4)

f'(0)  =  8 > 0 (Positive)

To the right of the critical point at x  =  2 :

Let x = 3 ∈ (2, 4)

f'(3)  =  -1 < 0 (Negative)

Result :

The curve is changing its direction from increasing to decreasing. So, there is relative maximum at x  =  c.

Relative minimum at x  =  1/2.

To the left of the critical point at x  =  4 :

Already taken and it is negative.

To the right of the critical point at x  =  4 :

Let x = 5 ∈ (4, ∞)

f'(x)  =  (x-2)(x-4)

f'(5)  =  (5-2)(5-4)

f'(5)  =  3 > 0 (Positive)

Result :

The curve is changing its direction from decreasing to increasing. So, there is relative minimum at x  =  c.

Relative minimum at x  =  4.

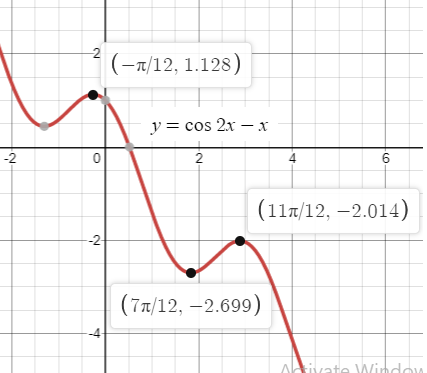
Example 3 :

The function defined by

f(x)  =  cos 2x - x

for all real values of x has relative maximum and relative minimum at x = ?.

Solution :

f(x)  =  cos 2x - x

f'(x)  =  -2sin 2x-1

f'(x)  =  0

-2sin 2x-1  =  0

2sin 2x+1  =  0

sin2x  =  -1/2

2x  =  sin^-1(-1/2) 

2x  =   -π/6, 7π/6

x  =   -π/12, 7π/12

The intervals are (0, -π/12) (-π/12, 7π/12) and (7π/12, 2π).

f'(x)  =  -2sin 2x-1

Let x = 14° ∈ (0, -π/12) 

f'(14)  =  positive

Let x = 104° ∈ (-π/12, 7π/12)

f'(104)  =  Negative

Let x = 150° ∈ (7π/12, 2π).

f'(150)  =  positive

Maximum at x = -π/12, minimum at x = 7π/12.

So, relative maximum at -π/12 + nπ and relative minimum at 7π/12 + nπ.

Example 4 :

The derivative f'(x) of a function f(x) is graphed below. Answer the questions about f(x).

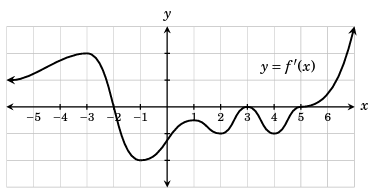
(a) State the critical points of f.

(b) State the interval(s) on which f increases.

(c) State the interval(s) on which f decreases.

(d) Does f have a local maximum? Where?

(e) Does f have a local minimum? Where?

Solution :

a)  When the given function is f(x), for what values of x, f'(x) = 0 those are critical numbers.

From the graph of first derivative finding the critical numbers :

• The x-intercepts in the first derivative graph is the critical numbers.
• By observing the graph given x-intercepts are -2, 3 and 5 are critical numbers.

b) By observing the graph of first derivative, for the intervals (-∞, -2) and (5, ∞) the graph is above the x-axis. So, it is increasing function in the interval (-∞, -2) and (5, ∞).

c)  By observing the graph of first derivative, for the intervals (-2, 5) the graph is below the x-axis. So, it is decreasing function in the interval (-2, 5).

(d) f'(x) changes from increasing to decreasing at x = -2. So, local maximum is at x = -2.

(e) f'(x) changes from decreasing to increasing at x = 5. So, local minimum is at x = 5.

Example 5 :

Use the 1st derivative test to find the relative extrema of the following function. Give only the x-coordinate of the extrema. Indicate your answer as relative max or min

f(x) = 5x²/(x - 2)²

Solution :

f(x) = 5x²/(x - 2)²

Using product rule, we find the first derivative.

u = 5x² and v = (x - 2)²

u' = 10x and v' = 2(x - 2)

f'(x) = [10x (x - 2)² - 5x² (2(x - 2))]/(x - 2)⁴

= [10x (x - 2)² - 10x² (x - 2)]/(x - 2)⁴

= 10(x - 2)[(x - 2) - x]/(x - 2)⁴

= -20/(x - 2)³

Vertical asymptote is at x = 2 and relative minimum at x = 0.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.