FINDING X AND Y INTERCEPTS AND FINDING EQUATION FROM INTERCEPTS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Question 1 :
Find the equation of the straight line whose x and y-intercepts on the axes are given by
(i) 2 and 3
(ii) -1/3 and 3/2
(iii) 2/5 and -3/4
Solution :
(i) 2 and 3
We can find the equation of the line using x and y intercepts, we can use the formula given below.
(x/a) + (y/b) = 1
here "a" stands for x-intercept and "b" stands for y-intercept.
(x/2) + (y/3) = 1
(3x + 2y)/6 = 1
3x + 2y = 6 (or) 3x + 2y - 6 = 0
(ii) -1/3 and 3/2
We can find the equation of the line using x and y intercepts, we can use the formula given below.
(x/a) + (y/b) = 1
here "a" stands for x-intercept and "b" stands for y-intercept.
x/(-1/3) + y/(3/2) = 1
(-3x/1) + (2y/3) = 1
(-9x + 2y)/3 = 1
-9x + 2y = 3
-9x + 2y - 3 = 0
9x - 2y + 3 = 0
Hence the required equation of the line is 9x - 2y + 3 = 0.
(iii) 2/5 and -3/4
a = 2/5 and b = -3/4
x/(2/5) + y/(-3/4) = 1
(5x/2) - (4y/3) = 1
(15x - 8y)/6 = 1
15 x - 8 y = 6
15x - 8y - 6 = 0
Hence the required equation of the line is 15x - 8y - 6 = 0.
Question 2 :
Find the x and y intercepts of the straight line
(i) 5x + 3y - 15 = 0 (ii) 2x - y + 16 = 0 (iii) 3x + 10y + 4 = 0
Solution :
(i) 5x + 3y - 15 = 0
To find the x and y intercepts from the given equation, we have to compare the given equation with the intercept form.
Intercept form of a line :
(x/a) + (y/b) = 1
5x + 3y - 15 = 0
5x + 3 y = 15
Divide the equation by 15
(5x/15) + (3y/15) = 15/15
(x/3) + (y/5) = 1
x-intercept = 3 and y -intercept = 5
(ii) 2x - y + 16 = 0
(x/a) + (y/b) = 1
2x - y = -16
Divide the equation by -16
(2x/(-16)) - (y/(-16)) = -16/(-16)
(x/(-8)) + (y/16) = 1
x-intercept = -8 and y -intercept = 16
(iii) 3x + 10y + 4 = 0
(x/a) + (y/b) = 1
3x + 10y = -4
Divide the equation by -4
(3x/(-4)) + (10y/(-4)) = -4/(-4)
x/(-4/3) + y/(-4/10) = 1
x/(-4/3) + y/(-2/5) = 1
x-intercept = -4/3 and y -intercept = -2/5
Question 3 :
If graphed, the ordered pairs in the table above would form a line. Where would this line intersect the x-axis?
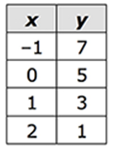
Solution :
By observing the table, one of the points on the line is (-1, 7) and y-intercept (when x = 0) is 5.
y = mx + b
x = -1, y = 7 and y-intercept (b) = 5
7 = m(-1) + 5
7 - 5 = -m
-m = 2
m = -2
y = -2x + 5
Question 4 :
Johanna picked 3 pounds of strawberries at a "pick-your-own" patch. At this particular patch, the cost is $1.50 for the pail and $3.99 per pound of strawberries picked. If a linear equation is created to represent the situation and written in the form y = mx+ b, which piece of the equation would the value 13.47 in this scenario most likely represent?
a) b b) m c) x d) y
Solution :
Cost of strawberries per pound = $3.99
Cost of 3 pounds of strawberries = 3(3.99)
= 11.97
Cost of pail = $1.50
Total cost = 11.97 + 1.50
y = 13.47
13.47 represents the value of variable y.
So, option d is correct.
Question 5 :
If the x-intercept of a line is positive and y-intercept is negative, does the line slant upward or downward from left to right? Explain your reasoning
Solution :
x-intercept = positive
y-intercept = negative
The required line is slant upward.
Question 6 :
A student says that the x-intercept of the graph x + 2y = 5 is the point (0, 5), why is the student incorrect ?
Solution :
x + 2y = 5
To find the x-intercept, we have to apply y = 0
Applying y = 0, we get
x + 2(0) = 5
x = 5
So, the x-intercept is (5, 0). The given point is (0, 5), then the student is incorrect.
Question 7 :
At which point does the graph of the equation 2x + y = 4 cross the x-axis ?
Solution :
2x + y = 4
Finding the point where it cross the x-axis, then put y = 0
2x + 0 = 4
2x = 4
x = 4/2
x = 2
Question 8 :
What is the y-intercept of the graph of the equation 3x + y = 6 ?
Solution :
3x + y = 6
To find y-intercept, put x = 0
3(0) + y = 6
0 + y = 6
y = 6
Question 9 :
Write the equation of a line in slope intercept form given a graph.
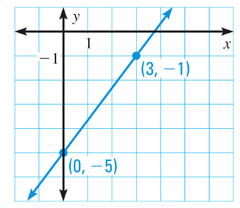
Solution :
Equation of line will be in the form y = mx + b
y-intercept (b) = -5
One of the point lies on the line is (3, -1)
-1 = m(3) - 5
-1 + 5 = 3m
3m = 4
m = 4/3
y = (4/3)x - 5
Question 10 :
Write the equation of a line in slope intercept form given a graph.
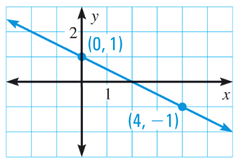
Solution :
Equation of line will be in the form y = mx + b
y-intercept (b) = 1
One of the point lies on the line is (4, -1)
-1 = m(4) + 1
-1 - 1 = 4m
4m = -2
m = -2/4
m = -1/2
y = (-1/2)x + 1
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus BC Problems with Solutions
Dec 20, 25 10:51 AM
AP Calculus BC Problems with Solutions -
AP Precalculus Problems and Solutions (Part - 1)
Dec 20, 25 10:49 AM
AP Precalculus Problems and Solutions (Part - 1) -
AP Calculus AB Problems with Solutions (Part - 1)
Dec 20, 25 10:49 AM
AP Calculus AB Problems with Solutions (Part - 1)
