FINDING WHETHER GIVEN LENGTHS ARE PYTHAGOREAN TRIPLES

What are Pythagorean triples ?

Pythagorean triples are the three positive integers that completely satisfy the Pythagorean theorem.

That is,

a² + b²  = c²

where,

c is the hypotenuse (or) longest side of the right  triangle.

a and b are the other two sides of lengths of the right triangle.

These three sides of the right triangle form the Pythagorean triples.

The Pythagorean triples are represented as {a, b, c}.

How to generate Pythagorean triples ?

If given any values of a Pythagorean triple, then the three integers can be generated by using the formula,

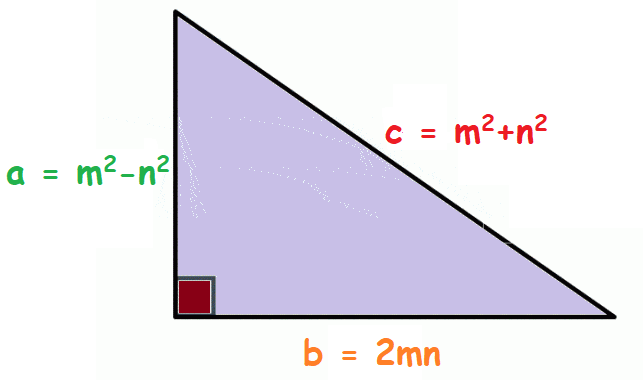
a = m² - n², b = 2mn, and c = m² + n².

(where m and n are positive integers, such that m > n)

Example 1 :

Find whether the lengths {5, 12, 13} is a Pythagorean triples.

Solution :

Let a  =  5, b  =  12, and c  =  13 be the lengths.

By Pythagorean theorem,

a² + b²  = c²

(5)² + (12)²  =  (13)²

25 + 144  =  169

169  =  169

So, {5, 12, 13} is a Pythagorean triples.

Example 2 :

Find whether the lengths {6, 1, 7} is a Pythagorean triples.

Solution :

Let a  =  6, b  =  1, and c  =  7 be the lengths.

By Pythagorean theorem,

a² + b²  = c²

(6)² + (1)²  =  (7)²

36 + 1  =  49

37 ≠ 49

So, {6, 1, 7} is not a Pythagorean triples.

Example 3 :

What is the Pythagorean triples using the values, m  =  7 and n  =  6 ?

Solution :

Given, values m  =  7 and n  =  6.

We are using the m and n values, to find the {a, b, c} of  Pythagorean triples.

Formula for generating Pythagorean triples,

Since (m > n),

a  =  m² - n², b  =  2mn, and c  =  m² + n²

Now, a  =  13, b  =  84, and c  =  85

So, {13, 84, 85} is the Pythagorean triples.

Example 4 :

What is the Pythagorean triples using the values, m  =  2 and n  =  1 ?

Solution :

Given, values m  =  2 and n  =  1.

We are using the m and n values, to find the {a, b, c} of  Pythagorean triples.

Formula for generating Pythagorean triples,

Since (m > n),

a  =  m² - n², b  =  2mn, and c  =  m² + n²

Now, a  =  3, b  =  4, and c  =  5

So, {3, 4, 5} is the Pythagorean triples.

Example 5 :

Find the missing side length, and if the side lengths form a Pythagorean triple. Explain.

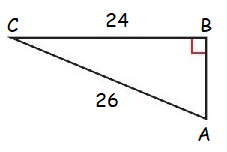
Solution :

Given, Hypotenuse side AC  =  26, Length₁ BC =  24 and Length₂ AB =  ?

Using Pythagorean theorem :

AB² + BC²  =  AC²

AB² + (24)²  =  (26)²

AB² + 576  =  676

AB²  =  100

AB  =  10

Length₂ AB =  10

So, the lengths are 10, 24, and 26.

Since the square of the hypotenuse side is equal to the sum of the square of the other two sides, it is a Pythagorean triple.

Example 6 :

{p, 144, 145} is a Pythagorean triple, What is the value of p ?

Solution :

Let a  =  p, b  =  144, and c  =  145 be the lengths.

By Pythagorean theorem,

a² + b²  = c²

p² + (144)²  =  (145)²

p² + 20736  =  21025

p²  =  21025 - 20736

p²  =  289

p  =  17

Now, {17, 144, 145} is a Pythagorean triple.

So, the value of p is 17.

Example 7 :

Joey tried a new route to reach his school today. He walked 6 blocks to the north, and then 8 blocks to the west. Find how far is his school from his home.

Solution :

The distance from the school to home is the length of the hypotenuse.

Let c be the missing distance from the school to home and a  =  6,  b  =  8

By Pythagorean theorem,

a² + b²  = c²

6² + 8²  =  c²

36 + 64  =  c²

100  =  c²

c  =  10

So, the distance from school to home is 10 blocks.

Example 8 :

Ms. Green tells you that a right triangle has a hypotenuse of 13 and a leg of 5. She asks you to find the other leg of the triangle. What is your answer?

Solution :

Let x be the other leg.

x² + 5² = 13²

x² + 25 = 169

x² = 169 - 25

x² = 144

x = √144

x = 12

Example 9 :

Two joggers run 8 miles north and then 5 miles west. What is the shortest distance, to the nearest tenth of a mile, they must travel to return to their starting point?

Solution :

Let x be the required distance.

x² + 5² = 8²

x² + 25 = 64

x² = 64 - 25

x² = 39

x = √39

x = 6.24 units

Example 10 :

Shown is a right angle triangle. Calculate:

(a) the perimeter of the triangle.

(b) the area of the triangle

Solution :

Let x be the third side of the triangle.

x² + 7² = 25²

x² + 49 = 625

x² = 625 - 49

x² = 576

x = √576

x = 24 units.

a) Perimeter of the triangle = 24 + 7 + 25

= 56 units

b) Area = (1/2) x base x height

= (1/2) x 24 x 7

= 12 x 7

= 84 square units.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.