FINDING TRIGONOMETRIC RATIOS FROM THE GIVEN TRIANGLE

Example 1 :

From the given figure, find all the trigonometric ratios of angle B.

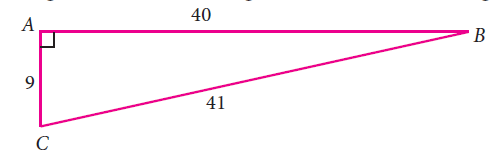
Solution :

Here we have to mark the angle at B.

From the given triangle,

Hypotenuse side (BC)  =  41

Opposite side (AC) =  9

Adjacent side (AB)  =  40

sin B =  Opposite side / Hypotenuse side

sin B  =  AC/BC  =  6/41

cos B =  Adjacent side / Hypotenuse side

cos B  =  AB/BC  =  40/41

tan B =  Opposite side / Adjacent side

tan B  =  AC/AB  =  6/40

cosec B  =  Hypotenuse side/Opposite side 

cosec B  =  BC/AC  =  41/6

sec B  =  Hypotenuse side/Adjacent side 

sec B  =  BC/AB  =  41/40

cot B  =  Adjacent side / Opposite side

cot B  =  AB/AC  =  40/6

Example 2 :

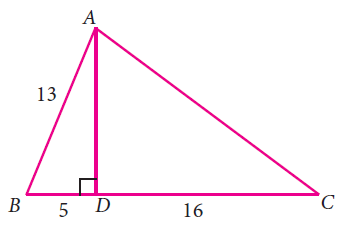
From the given figure, find the values of

(i) sin B (ii) sec B (iii) cot B

(iv) cos C (v) tan C (vi) cosec C

Solution :

In triangle ABD,

AB²  =  AD² + BD²

13²  =  AD² + 5²

169 - 25  = AD²

AD²  =  144

AD  =  12

In triangle ADC,

AC²  =  AD² + DC²

AC²  =  12² + 16²

AC²  =  144 + 256

AC  =  20

Example 3 :

If 2 cos θ = √3, then find all the trigonometric ratios of angle θ.

Solution :

cos θ = √3/2  =  Adjacent side / Hypotenuse side

(Opposite side)²  =  (Hypotenuse side)² - (Adjacent side)²

(Opposite side)²  =  2² - (√3)²   =  4 - 3

Opposite side  =  1

sin A = Opposite side / Hypotenuse  =  1/2

cos A  =  Adjacent side / Hypotenuse  =  √3/2

tan A  =  Opposite side / Adjacent side  = 1/√3

cosec A  = Hypotenuse / Opposite side  = 2/1

sec A  =  Hypotenuse / Adjacent side  =  2/√3

cot A  =  Adjacent side / Opposite side  =  √3/1

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.