FINDING THE VOLUME OF A SPHERE WORKSHEET

Question 1-3 : Find the volume of sphere shown below. Round your answer to the nearest tenth if necessary. Use the approximate of value of π, that is 3.14.

Question 1 :

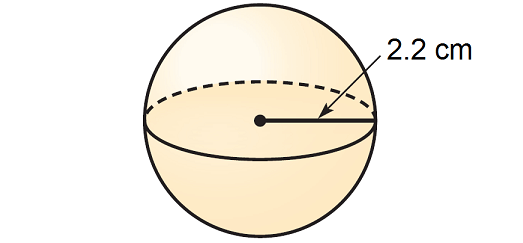
Question 2 :

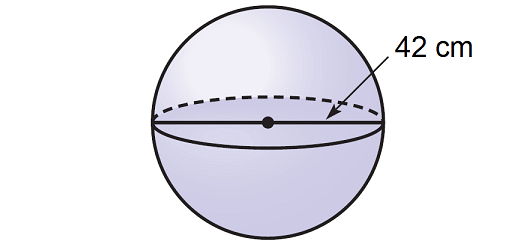
Question 3 :

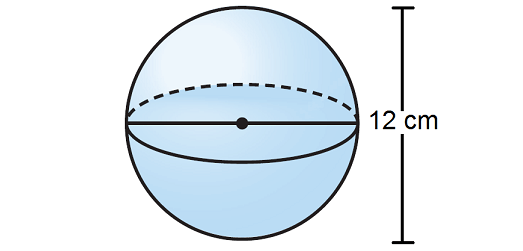
Question 4 :

The globe of the Moon has a radius of 10 inches. Find the volume of the globe. Round your answer to the nearest whole number.

Question 5 :

Find the radius of the sphere with the given volume.

a)  Volume = 972π mm³

b)  Volume = 4.5π cm³

Question 6 :

Find the volume of the composite solid. Round your answer to the nearest tenth.

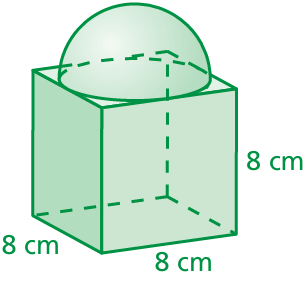
Question 7 :

Your friend says that the volume of a sphere with radius r is four times the volume of a cone with radius r. When is this true? Justify your answer.

Question 8 :

A right circular cylindrical container of base radius 6 cm and height 15 cm is full of ice cream. The ice cream is to be filled in cones of height 9 cm and base radius 3 cm, having a hemispherical cap. Find the number of cones needed to empty the container.

Question 9 :

A solid sphere of radius 6 cm is melted into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 5 cm and its height is 32 cm, then find the thickness of the cylinder.

Question 10 :

A hemispherical bowl is filled to the brim with juice. The juice is poured into a cylindrical vessel whose radius is 50% more than its height. If the diameter is same for both the bowl and the cylinder then find the percentage of juice that can be transferred from the bowl into the cylindrical vessel.

1. Answer :

Step 1 :

Write the formula to find volume of a sphere.

V = 4/3 ·  πr³

Step 2 :

Substitute the given measures.

V ≈ 4/3 · 3.14 · (2.2)³

Simplify.

V ≈ 4/3 · 3.14 · 10.648

V ≈ 44.6

So, the volume of the given sphere is about 44.6 cubic cm.

2. Answer :

Step 1 :

Write the formula to find volume of a sphere.

V = 4/3 ·  πr³ -----(1)

Step 2 :

To find the volume, we need the radius of the sphere. But, the diameter is given, that is  42 cm. So, find the radius.

r = diameter/2

r = 42/2

r = 21

Step 3 :

Substitute π ≈ 3.14 and r = 21 in (1).

V ≈ 4/3 · 3.14 · 21³

Simplify.

V ≈ 4/3 · 3.14 · 9261

V ≈ 38,772.7

So, the volume of the given sphere is about 38,772.7 cubic cm.

3. Answer :

Step 1 :

Write the formula to find volume of a sphere.

V = 4/3 ·  πr³ -----(1)

Step 2 :

To find the volume, we need the radius of the sphere. But, the height is given, that is  12 cm. 

We know that the height of a sphere equals twice the radius. 

That is,

h = 2r

Substitute h  =  12.

12 = 2r

Divide both sides by 2.

12/2 = 2r/2

6 = r

Step 3 :

Substitute π ≈ 3.14 and r = 6 in (1).

V ≈ 4/3 · 3.14 · 6³

Simplify.

V ≈ 4/3 · 3.14 · 216

V ≈ 904.3

So, the volume of the given sphere is about 904.3 cubic cm.

4. Answer :

Radius = 10 inches 

Volume of sphere = 4/3 · (πr³)

= (4/3) · 3.14 · (10)³

= 4186.6 cm³

5. Answer :

Find the radius of the sphere with the given volume.

a)  Volume = 972π mm³

 4/3 · (πr³) = 972π

(4/3) r³ = 972

r³ = 972 (3/4)

r³ = 729

r = ∛729

r = ∛(7 x 7 x 7)

r = 7 cm

So, the required radius is 7 cm.

b)  Volume = 4.5π cm³

 4/3 · (πr³) = 4.5 π

(4/3) r³ = 4.5

r³ = 4.5 (3/4)

r³ = 3.375

r = ∛3.375

r = 1.5 cm

So, the required radius is 1.5 cm.

6. Answer :

Volume of composite figure

= volume of cube + volume of hemisphere

= a³ + (2/3) (πr³)

raius = 8/2 = 4 cm

= 4³ + (2/3) (π (8)³)

= 64 + (2/3) x 3.14 x 512

= 64 + 1071.7

= 1135.7 cm³

7. Answer :

Volume of sphere = (4/3) (πr³)

Volume of cone = (1/3) (πr²h)

Volume of sphere = 4 x Volume of cone

(4/3) (πr³) = 4(1/3) (πr²h)

(4/3) (πr³) = (4/3) (πr²h)

r = h 

The given statement will become true when radius of sphere and cone both are equal.

8. Answer :

radius of cylinder = 6 cm

height = 15 cm

radius of cone = 3 cm = radius of sphere

height of cone = 9 cm

Number of cones to be filled

= volume of cylinder / (volume of cone + volume of hemisphere)

= (πr²h) / (1/3) (πr²h) + (2/3) (πr³)

= (6² x 15) / [(1/3) r²(h + 2r)]

= (3 x 6² x 15) / [3²(9 + 6)]

= (3 x 36 x 15) / [9 x 15]

= 12 cones

9. Answer :

Volume of sphere = volume of hollow cylinder

(4/3) (πr³) = π(R² - r²) h

Radius of sphere = 6 cm

External radius of cylinder = 5 cm

Height of cylinder = 32 cm

Let r be the inner radius of cyclinder.

(4/3) (6³) = (5² - r²) x 32

5² - r² = (4/3) (216/32)

25 - r² = 9

25 - 9 = r²

r² = 16

r = 4

Thickness = R - r

= 5 - 4

= 1 cm

So, the thickness of the cylinder is 1 cm.

10. Answer :

Quantity of juice in the hemispherical bowl = (2/3) (πr³)

r and h be the radius and height of cylinder

r = 150% of h

r = 3h/2

Volume of hemispherical bowl = (2/3) (π(3h/2)³)

= (2/3) π(27h³/8)

(9/4)πh³

Quantity if juice in cylindrical container = πr²h

= π(3h/2)²h

= (9/4)πh³

So, it is possible to transfer the full quantity from one container to another.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.