FINDING THE VOLUME OF A CYLINDER

Finding volumes of cylinder is similar to finding volumes of prisms. We can find the volume V of both a prism and a cylinder by multiplying the height by the area of the base. 

Let the area of the base of a cylinder be B and the height of the cylinder be h. Write a formula for the cylinder’s volume V.

V  =  Bh

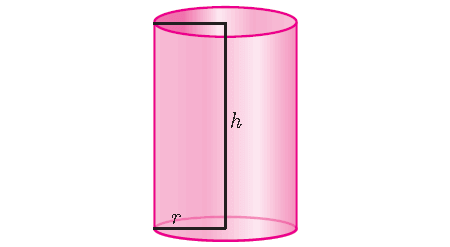
The base of a cylinder is a circle, so for a cylinder,

B  =  πr²

Then, we have

V = πr²h cubic units

Example 1 :

Find the volume of the cylinder given below. Round your answer to the nearest tenth if necessary. Use the approximate of value of π, that is 3.14. 

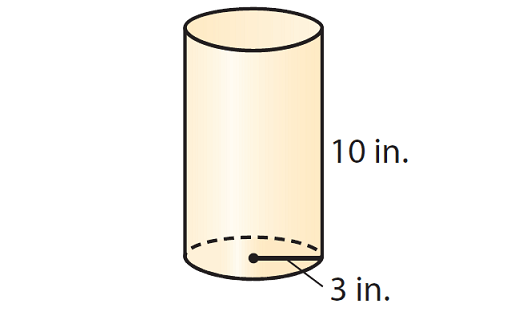
Solution :

Step 1 : 

Write the formula to find volume of a cylinder

V = πr²h cubic units

Step 2 : 

Substitute the given measures. 

V ≈ 3.14 · 3² · 10

Simplify.

V ≈ 3.14 · 9 · 10

V ≈ 282.6

So, the volume of the given cylinder is about 282.6 cubic inches. 

Example 2 :

Find the volume of the cylinder given below. Round your answer to the nearest tenth if necessary. Use the approximate of value of π, that is 3.14. 

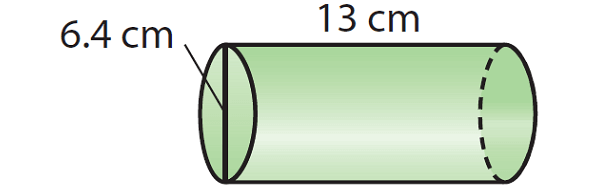
Solution :

Step 1 : 

Write the formula to find volume of a cylinder

V = πr²h cubic units -----(1)

Step 2 : 

To find the volume, we need the radius of the cylinder. But, the diameter is given, that is 6.4 cm. So, find the radius. 

r = diameter / 2

r = 6.4/2

r = 3.2

Step 3 : 

The given cylinder is in horizontal position and its length is 13 cm. If the cylinder is in vertical position, the length will become height. So, the height is 

h = 13

Step 4 :

Substitute π ≈ 3.14, r = 3.2 and h = 13 in (1).

V ≈ 3.14 · (3.2)² · 13

Simplify.

V ≈ 3.14 · 10.24 · 13

V ≈ 418

So, the volume of the given cylinder is about 418 cubic cm. 

Example 3 :

Find the volume of the cylinder given below. Round your answer to the nearest tenth if necessary. Use the approximate of value of π, that is 3.14. 

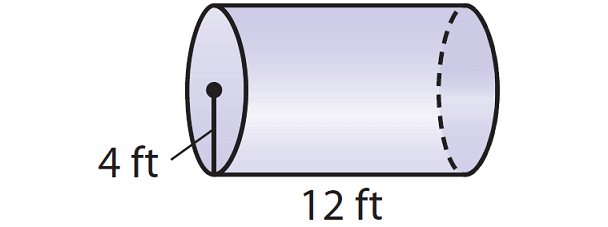
Solution :

Step 1 : 

Write the formula to find volume of a cylinder

V = πr²h cubic units -----(1)

Step 2 : 

The given cylinder is in horizontal position and its length is 12 ft. If the cylinder is in vertical position, the length will become height. So, the height is 

h = 12

Step 3 : 

Substitute π ≈ 3.14, r = 4 and h = 12 in (1). 

V ≈ 3.14 · 4² · 12

Simplify.

V ≈ 3.14 · 16 · 12

V ≈ 602.9

So, the volume of the given cylinder is about 602.9 cubic feet. 

Example 4 :

Find the volume of the cylinder given below. Round your answer to the nearest tenth if necessary. Use the approximate of value of π, that is 3.14. 

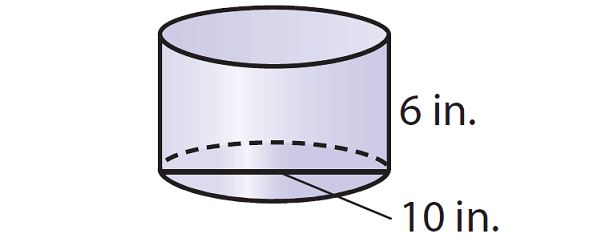
Solution :

Step 1 : 

Write the formula to find volume of a cylinder

V = πr²h cubic units -----(1)

Step 2 : 

To find the volume, we need the radius of the cylinder. But, the diameter is given, that is 10 cm. So, find the radius. 

r = diameter / 2

r = 10/2

r = 5

Step 2 : 

Substitute π ≈ 3.14, r = 5 and h = 6 in (1). 

V ≈ 3.14 · 5² · 6

Simplify.

V ≈ 3.14 · 25 · 6

V ≈ 471

So, the volume of the given cylinder is about 471 cubic inches. 

Example 5 :

How much salsa is missing from the jar?

Solution :

Height of salsa in cylindrical jar = 10 - 4

= 6 cm

radius = 5 cm

Volume = base area x height

= πr²h

= 3.14 (5)²(6)

= 471 cm³

Example 6 :

About how many gallons of water does the water cooler bottle contain? (1 ft³ ≈ 7.5 gal)

a)  5.3 gal    b) 10 gal    c) 17 gal    d) 40 gal

Solution :

Volume of cooler bottle = πr²h

r = 1/2

= 0.5 ft

height = 1.7 ft

= 3.14 x (0.5)² x 1.7

= 1.3345 cm³

1 ft³ = 7.5 gallon

1.3345 ft³ = 1.3345 x 7.5

= 10.00875 gallons

Approximately 10 gallons.

Example 7 :

A cylindrical swimming pool has a diameter of 16 feet and a height of 4 feet. About how many gallons of water can the pool contain? Round your answer to the nearest whole number. (1 ft³ ≈ 7.5 gal)

Solution :

Volume of swimming pool = πr²h

r = 16/2 ==> 8 feet

height = 4 feet

Volume = 3.14 x 8² x 4

= 803.84 ft³

1 ft³ ≈ 7.5 gal

803.84 ft³ = 803.84 x 7.5

= 6028.8 gallons

Example 8 :

A cylinder has a surface area of 1850 square meters and a radius of 9 meters. Estimate the volume of the cylinder to the nearest whole number.

Solution :

Surface area of cylinder = 1850 square meter

radius = 9 meter

2πrh = 1850

2 x 3.14 x 9 x h = 1850

h = 1850 / (2 x 3.14 x 9)

= 32.73

Volume of cylinder = πr²h

= 3.14 x 9² x 32.73

= 8324.5482 m³

So, the required volume of the cylinder is 8325 m³

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.