FINDING THE VOLUME OF A CYLINDER WORKSHEET

1. Find the volume of the cylinder given below. Round your answer to the nearest tenth if necessary. Use the approximate of value of π, that is 3.14.

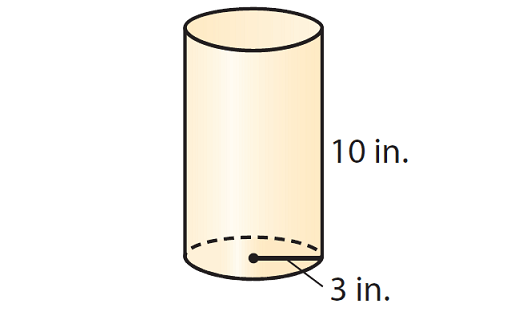
2. Find the volume of the cylinder given below. Round your answer to the nearest tenth if necessary. Use the approximate of value of π, that is 3.14.

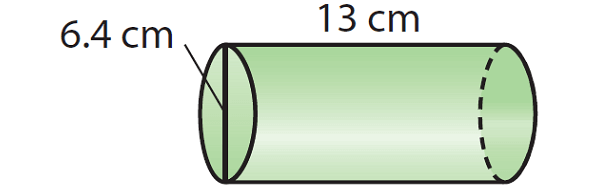
3. Find the volume of the cylinder given below. Round your answer to the nearest tenth if necessary. Use the approximate of value of π, that is 3.14.

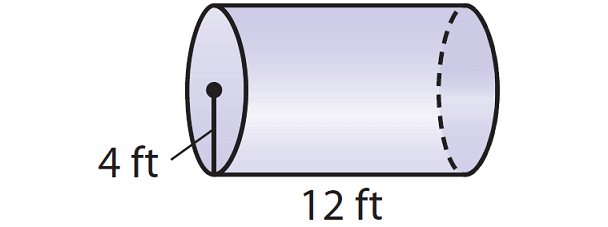
4. Find the volume of the cylinder given below. Round your answer to the nearest tenth if necessary. Use the approximate of value of π, that is 3.14.

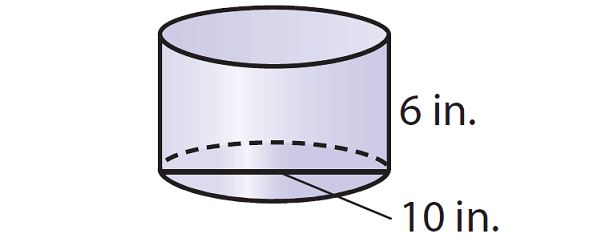
5. A cylinder has a radius of 12 inches and a height of 14 inches. What is the volume of this cylinder?

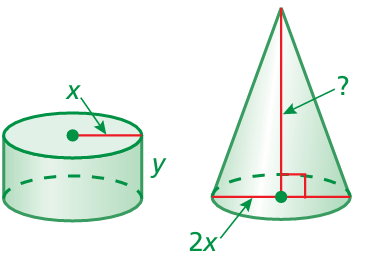
6. Cone A has the same height but twice the radius of Cone B. What is the ratio of the volume of Cone A to the volume of Cone B?

7. If the radius of a right circular cylinder is decreased by 50% and its height is increased by 60%, its volume will be decreased by

a)  10%      b)  60%    c)  40%       d)  20%

8. A cylindrical container of three rubber balls has a height of 18 centimeters and a diameter of 6 centimeters. Each ball in the container has a radius of 3 centimeters. Find the amount of space in the container that is not occupied by rubber balls. Round your answer to the nearest whole number.

1. Answer :

Step 1 :

Write the formula to find volume of a cylinder.

V = πr²h cubic units

Step 2 :

Substitute the given measures.

V ≈ 3.14 · 3² · 10

Simplify.

V ≈ 3.14 · 9 · 10

V ≈ 282.6

So, the volume of the given cylinder is about 282.6 cubic inches.

2. Answer :

Step 1 :

Write the formula to find volume of a cylinder.

V = πr²h cubic units -----(1)

Step 2 :

To find the volume, we need the radius of the cylinder. But, the diameter is given, that is 6.4 cm. So, find the radius.

r = diameter/2

r = 6.4/2

r = 3.2

Step 3 :

The given cylinder is in horizontal position and its length is 13 cm. If the cylinder is in vertical position, the length will become height. So, the height is

h = 13

Step 4 :

Substitute π ≈ 3.14, r = 3.2 and h = 13 in (1).

V ≈ 3.14 · (3.2)² · 13

Simplify.

V ≈ 3.14 · 10.24 · 13

V ≈ 418

So, the volume of the given cylinder is about 418 cubic cm.

3. Answer :

Step 1 :

Write the formula to find volume of a cylinder.

V = πr²h cubic units -----(1)

Step 2 :

The given cylinder is in horizontal position and its length is 12 ft. If the cylinder is in vertical position, the length will become height. So, the height is

h = 12

Step 3 :

Substitute π ≈ 3.14, r = 4 and h = 12 in (1).

V ≈ 3.14 · 4² · 12

Simplify.

V ≈ 3.14 · 16 · 12

V ≈ 602.9

So, the volume of the given cylinder is about 602.9 cubic feet.

4. Answer :

Step 1 :

Write the formula to find volume of a cylinder.

V = πr²h cubic units -----(1)

Step 2 :

To find the volume, we need the radius of the cylinder. But, the diameter is given, that is 10 cm. So, find the radius.

r = diameter/2

r = 10/2

r = 5

Step 2 :

Substitute π ≈ 3.14, r = 5 and h = 6 in (1).

V ≈ 3.14 · 5² · 6

Simplify.

V ≈ 3.14 · 25 · 6

V ≈ 471

So, the volume of the given cylinder is about 471 cubic inches.

5. Answer :

Radius = 12 inches and height = 14 inches

Volume of cylinder = πr²h 

= 3.14 (12)² (14)

= 6330.24 cubic inches.

6. Answer :

Cone A has the same height but twice the radius of Cone B. What is the ratio of the volume of Cone A to the volume of Cone B?

Volume of cylinder :

Radius = x and height = y

Volume = πr²h 

= πx²y

Volume of cone :

Radius = 2x/2 ==> x and height = y

Volume = (1/3) πr²h 

= (1/3) πx²y

πx²y : (1/3) πx²y

3 : 1

So, the required ratio is 3 : 1

7. Answer :

Let r and h be the radius and height of the cyllinder

After the meausres has been changed :

Radius = 50% of r

height = 160% of h

Volume of new cylinder = πr²h 

= π(0.50r)²(1.60h)

= π(0.25r²)(1.60h)

= 0.40πr² h

= 40% πr² h

= 40% of volume of old cylinder

So, option c is correct.

8. Answer :

Volume of cylinder = πr²h 

Volume of sphere = (4/3) πr³

the amount of space in the container that is not occupied by rubber balls

= πr²h - 3 x (4/3) πr³

= πr²h - 4πr³

Radius of cylinder = 6/2 ==> 3 cm

height of cylinder = 18 cm

Radius of sphere = 3 cm

= π(3² x 18 - 4(3)³)

= π(162 - 108)

= π 54

= 54(3.14)

= 169.56 cm³

Approximately 170 cm³

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.