FINDING THE VOLUME OF A CONE

We can find the volume of a sphere using the volume of a cylinder.

Cylinder is a solid which has a circular base.

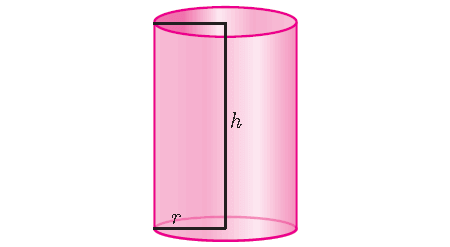
We know the fact that the volume of any solid is equal to the product of base area and height of the solid.

So, the volume of a right circular cylinder of base radius ‘r’ and height ‘h’ is given by

V = (Base Area) x (Height)

The base of a cylinder is a circle, so for a cylinder,

Base Area = πr²

Therefore, 

Volume of a cylinder = πr²h cubic units

Consider a right circular cylinder and three right circular cones of same base radius and height as that of the cylinder.

The contents of three cones will exactly occupy the cylinder.

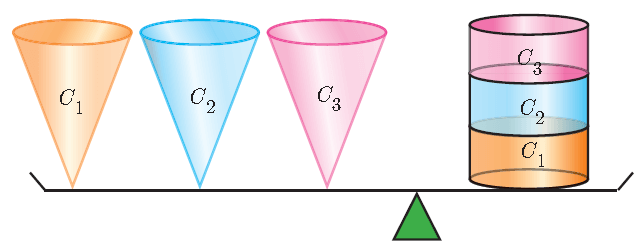
Then,

When we model the volume of a sphere, we will be getting the following result. 

3 x (Volume of a cone) = Volume of cylinder

3 x (Volume of a cone) = πr²h

Volume of the cone = 1/3 · πr²h cubic units

Example 1 :

Find the volume of the cone given below. Round your answer to the nearest tenth if necessary. Use the approximate of value of π, that is 3.14. 

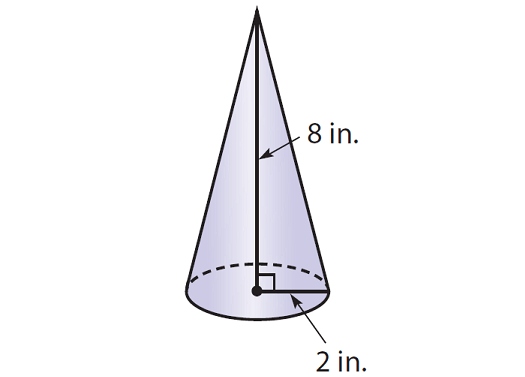
Solution :

Step 1 :

Write the formula to find volume of a cone.

V = 1/3 · πr²h

Step 2 :

Substitute the given measures.

V ≈ 1/3 · 3.14 · 2² · 8

Simplify.

V ≈ 1/3 · 3.14 · 4 · 8

V ≈ 33.5

So, the volume of the given cone is about 33.5 cubic inches.

Example 2 :

Find the volume of the cone given below. Round your answer to the nearest tenth if necessary. Use the approximate of value of π, that is 3.14.

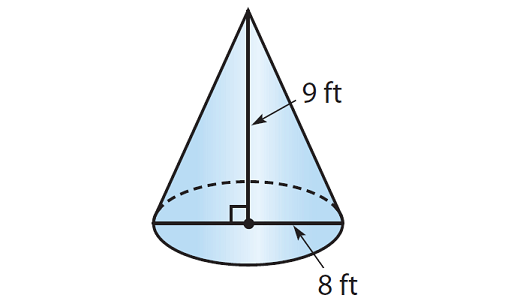
Solution :

Step 1 :

Write the formula to find volume of a cone.

V = 1/3 · πr²h -----(1)

Step 2 :

To find the volume, we need the radius of the cone. But, the diameter is given, that is 8 ft. So, find the radius. 

r = diameter / 2

r = 8/2

r = 4

Step 3 :

Substitute π ≈ 3.14, r = 4 and h = 9 in (1).

V ≈ 1/3 · 3.14 · 4² · 9

Simplify.

V ≈ 1/3 · 3.14 · 16 · 9

V ≈ 150.7

So, the volume of the given cone is about 150.7 cubic feet.

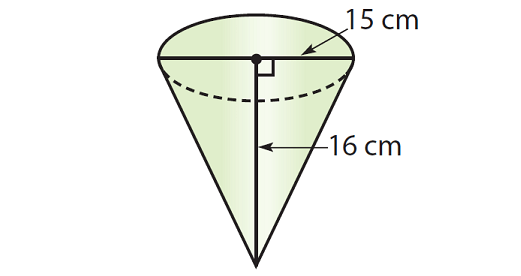
Example 3 :

Find the volume of the cone given below. Round your answer to the nearest tenth if necessary. Use the approximate of value of π, that is 3.14. 

Solution :

Step 1 :

Write the formula to find volume of a cone.

V = 1/3 · πr²h -----(1)

Step 2 :

To find the volume, we need the radius of the cone. But, the diameter is given, that is 15 cm. So, find the radius. 

r = diameter / 2

r = 15/2

r = 7.5

Step 3 :

Substitute π ≈ 3.14, r = 7.5 and h = 16 in (1).

V ≈ 1/3 · 3.14 · 7.5² · 16

Simplify.

V ≈ 1/3 · 3.14 · 56.25 · 16

V ≈ 942

So, the volume of the given cone is about 942 cubic cm. 

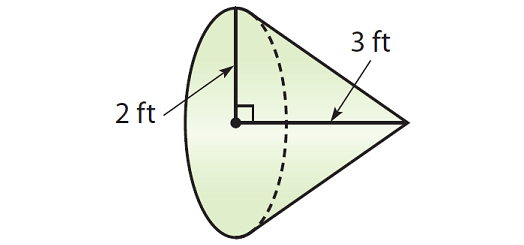
Example 4 :

Find the volume of the cone given below. Round your answer to the nearest tenth if necessary. Use the approximate of value of π, that is 3.14. 

Solution :

Step 1 :

Write the formula to find volume of a cone.

V = 1/3 · πr²h

Step 2 :

Substitute the given measures. 

V ≈ 1/3 · 3.14 · 2² · 3

Simplify.

V ≈ 1/3 · 3.14 · 4 · 3

V ≈ 12.6

So, the volume of the given cone is about 12.6 cubic feet.

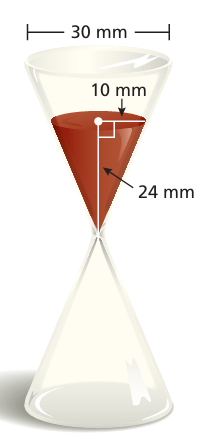
Example 5 :

You must answer a trivia question before the sand in the timer falls to the bottom. The sand falls at a rate of 50 cubic millimeters per second. How much time do you have to answer the question?

Solution :

Volume of sand in the bottle = (1/3) · πr²h

radius = 10 mm and height = 24 mm

= (1/3) x 3.14 x 10² x 24

= 3.14 x 100 x 8

= 2512 mm³

Quantity of sand falls per second = 50 cubic mm

Time taken = 2512 / 50

= 50.24 seconds

Example 6 :

Describe and correct the error in finding the volume of the cone.

Solution :

Radius = 6/2 ==> 3 m

Height = 8 m

Volume of cone = π x 3² x 24

= 216π m³

The error is instead of applying radius as 3 m, it is been applies as 6 m. That is the error.

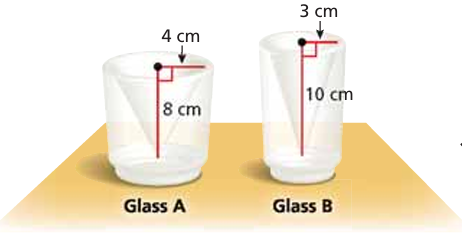
Example 7 :

The inside of each glass is shaped like a cone. Which glass can hold more liquid? How much more?

Solution :

Quantity of liquid in glass A = (1/3) · πr²h

r = 4 cm and h = 8 cm

= (1/3) · 3.14 x 4² x 8

= 133.97 cm³

Quantity of liquid in glass B = (1/3) · πr²h

r = 3 cm and h = 10 cm

= (1/3) · 3.14 x 3² x 10

= 94.2 cm³

Glass A will contain more lquid.

Example 8 :

The volume of a cone is 20 π cubic meters. What is the volume of a cylinder having the same base and same height?

Solution :

Volume of cone = 20 π cubic meters

(1/3) · πr²h = 20 π

From the given information, we know that raius and height of cone and radius and height of cylinder both are equal.

πr²h = 20 π (3)

Volume of cylinder = 60π

Example 9 :

Water leaks from a crack in a vase at a rate of 0.5 cubic inch per minute. How long does it take for 20% of the water to leak from a full vase?

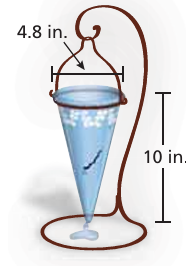
Solution :

Quantity of water in the vase = (1/3) · πr²h

r = 2.4 in and h = 10 in

= (1/3) x 3.14 x 2.4²x 10

= 60.288 cubic inches

20% of water = 0.20 (60.288)

= 12.0576 cubic inches

Speed of leakage = 0.5 inch per minute

Time taken to have a leakage of 12.0576 cubic inches

= 12.0576/0.5

= 24.1152 minutes

Approximately 24 minutes.

Example 10 :

The circumference of the base of the cone is 6π inches. What is the volume of cone in terms of π when the height is 13 inches.

Solution :

Circumference of base = 6π

2 π r = 6 π

2r = 6

r = 3

Volume of cone = (1/3) · πr²h

= (1/3) · π · 3²(13)

= 39 π cubic inches.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.