FINDING THE VERTEX FOCUS DIRECTRIX AND LATUS RECTUM OF THE PARABOLA

In this section, you will learn to find vertex, focus, equation of directrix and length of latus rectum of the parabola.

Before seeing example problems, let us remember some basic concepts about parabola. 

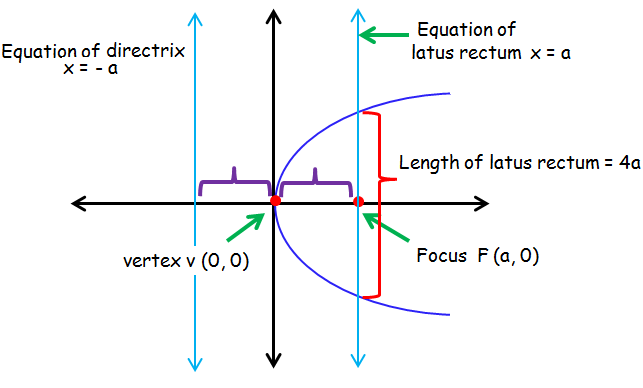
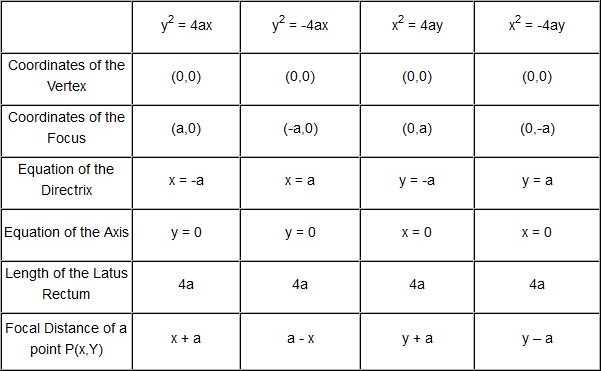
Parabola symmetric about x-axis and open right ward :

Standard form of parabola

y²  =  4ax

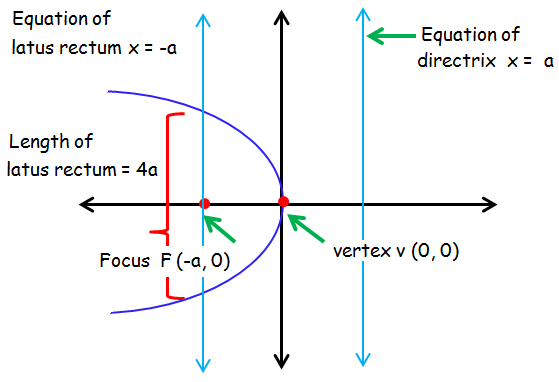
Parabola symmetric about x-axis and open left ward :

Standard form of parabola

y²  =  -4ax

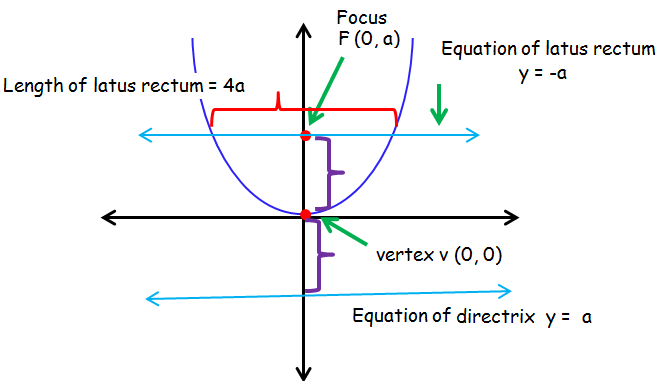
Parabola symmetric about y-axis and open up ward :

Standard form of parabola

x²  =  4ay

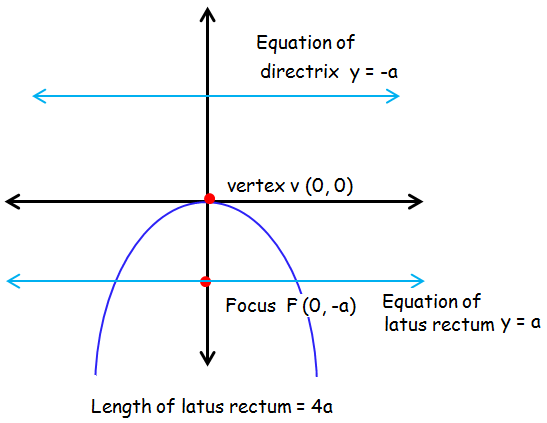
Parabola symmetric about y-axis and open down ward :

Standard form of parabola

x²  =  -4ay

Now let us see some examples based on the above concept.

Example 1 :

Find the focus, vertex, equation of directrix and length of the latus rectum of the parabola

y²  =  12x

Solution :

From the given equation, the parabola is symmetric about x - axis and it is open right ward.

y²  =  12x

4a  =  12

a  =  3

Vertex : V (0, 0)

Focus : F (3, 0)

Equation of directrix : x  =  -3

Length of latus rectum :  4a  =  4(3)  ==> 12

Example 2 :

Find the focus, vertex, equation of directrix and length of the latus rectum of the parabola

y²  =  -8x

Solution :

From the given equation, the parabola is symmetric about x - axis and it is open left ward.

y²  =  -8x

4a  =  8

a  =  2

Vertex : V (0, 0)

Focus : F (-2, 0)

Equation of directrix : x  =  2

Length of latus rectum :  4a  =  4(2)  ==> 8

Example 3 :

Find the focus, vertex, equation of directrix and length of the latus rectum of the parabola

y² - 8x - 2y + 17  =  0

Solution :

The given equation in not in standard form. So, first let us convert it into standard form.

y² - 2y  =  8x - 17

(y - 1)² - 1  =  8x - 17

(y - 1)²  =  8x - 17 + 1

(y - 1)²  =  8x - 16

(y - 1)²  =  8(x - 2)

The parabola is symmetric about x - axis and it is open right ward.

Let X  =  x -  2 and Y  =  y - 1

By replacing X and Y, we get

Y²  =  8X

4a  =  8

a  =  2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.